Uma viga homogênea de de comprimento e de peso está suspensa horizontalmente. No lado esquerdo está presa a uma parede por uma dobradiça; no lado direito é sustentada por um cabo pregado na parede a uma distância acima da viga. A tensão de ruptura do cabo é . (a) Que valor de corresponde a essa tensão? (b) Para que o cabo não se rompa, deve aumentar ou diminuir em relação a esse valor?
Passo 1
Falaaaa galerinha do RespondeAí, show de bolinhas com vocês?
Se liga só, nesse exercício aqui a gente precisa determinar a distância que uma viga deve estar suspensa através de um cabo como na figura abaixo:
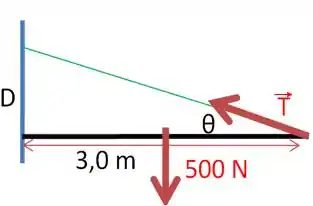
Onde é a tensão exercida pelo cabo na viga, enquanto que a força de é a força peso da viga.
Sabendo disso, podemos utilizar as equações do equilíbrio para calcular a distância que aguenta a tensão máxima no cabo.
Passo 2
Show de bolinhas, pra facilitar nossas contas, como não conhecemos as forças de apoio que atuam na dobradiça, podemos calcular o somatório dos torque em relação ao ponto que passa pela dobradiça na viga. Teremos que:
Sendo assim:
Como queremos a tensão máxima de ruptura , podemos isolar , de modo que:
Segue que:
Logo:
Passo 3
A malandragem disso tudo, é que a viga e parede de tamanho formam um triângulo retângulo, então podemos aplicar as relações trigonométricas para descobrir a distância , como elas formam o cateto oposto e o cateto adjacente podemos usar a relção com a tangente, tal que:
Como vimos que , vamos obter que:
Portanto:
Passo 4
Belezera, agora na letra (b), queremos saber se para que o cabo não se rompa, deve aumentar ou diminuir em relação ao valor que acabamos de encontrar. Pra isso, podemos pegar primeiro a relação que encontramos no Passo 2, entre o seno e tensão :
Se a gente isolar , teremos:
Isso quer dizer, que a tensão diminui, a medida que aumenta, ou melhor, se aumenta isso quer dizer que o ângulo está aumentando. De modo que podemos reescrever nossa frase como:
A tensão diminui, a medida que o ângulo aumenta. Portanto, se a gente quer que o ângulo aumente, o distância deve aumentar.
Resposta
(a)
(b)Aumentar