Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 14.1 - Ex. 46
Um objeto de oscila em uma mesa horizontal sem atrito presa na extremidade de uma mola com uma amplitude de sua aceleração máxima é . Encontre a energia mecânica total
Passo 1
Oláaa, querido! Ele quer a energia mecânica total do sistema. Ela é dada de forma geral por
Onde é a energia cinética e é a energia potencial.
Para resolver essa, a gente pode achar a energia potencial do objeto quando ele está na distância máxima da posição de equilíbrio, ou seja, quando ou .
Por que? Porque nessa posição temos a aceleração máxima que o enunciado dá e a velocidade é nula.
Se a velocidade é nula, então não há energia cinética, e se não há energia cinética, a energia total fica
E esse é a energia potencial da mola, que tem a fórmulinha:
E como a gente quer a energia quando ou (posição de velocidade nula), essa fórmula fica
Falta só achar . Bora então calcular isso aí? Bora!
Passo 2
Olha diagrama de corpo livre do objeto:
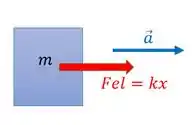
Essa é a força elástica.
Pela Segunda Lei de Newton:
Sendo que é a massa do objeto. Como não temos o valor da constante de força da mola, vamos isolar ela:
E quando a aceleração é máxima , ou . Vamos usar o valor positivo para as contas ficarem fofas, a equação da constante então fica:
Passo 3
Substituindo na equação da energia mecânica total:
Substituindo cada um dos valores dados, lembrando que :
Passando o que está em para metros, para sairmos com a reposta em joules certinho