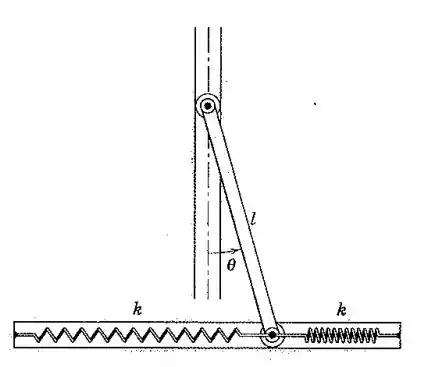
As extremidades da barra uniforme de massa m deslizam livremente nas ranhuras vertical e horizontal, como mostrado. Se a barra está em equilíbrio estático quando , determine a frequência natural das pequenas oscilações. Que condição deve ser imposta sobre a constante de mola a fim de que ocorram oscilações?

Bom pessoal, é importante analisar o centro de massa do sistema, que no caso é o centro da barra. Para descobrir a velocidade do centro de massa G, podemos usar o conceito de centro instantâneo de velocidade nula. Veja o diagrama:

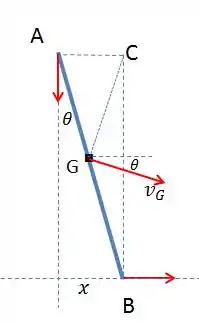
Como A só pode se movimentar dentro da ranhura vertical, sua velocidade deve também deve estar nessa direção. A mesma coisa vale para o ponto B. Desta forma, podemos traçar perpendiculares aos vetores velocidades e encontrar o centro instantâneo C. A partir de C, traçamos uma reta até o centro de massa G e enfim podemos traçar sua velocidade perpendicular a esta reta. Podemos então escrever na forma da equação:

Agora vamos para a parte de energia.

Como sabemos, em um movimento harmônico simples, a energia é um balanço entre a energia cinética e a energia potencial, como mostra a equação:

Como o sistema é conservativo, a energia total E é uma constante. Além disso, nós temos que quando a energia cinética é máxima, a energia potencial é nula, e vice versa. Veja só:

Como o exercício não diz nada quando podemos considerar que neste instante as molas estão em seu comprimento natural. Portanto, a energia potencial elástica será nula:

Agora, vamos voltar para a equação do movimento harmônico e escrever de uma maneira mais completa de acordo com a questão.

Onde a energia cinética é composta pela energia cinética rotacional e pela energia cinética de translação .

Agora, a energia potencial neste caso é composta pela gravitacional e pela elástica das molas. Quando o ângulo aumentar, o centro de massa da barra vai descer o equivalente à , como pode ser visto pelo diagrama abaixo. Já a energia potencial elástica, basta somar as deflexões das duas molas. A equação fica então:

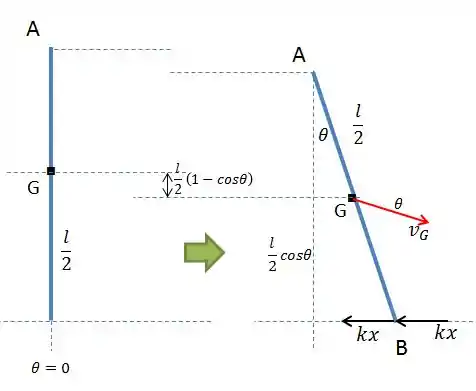
Para verificar se a equação está correta, teste se Hehe

OBS: O sinal da energia potencial gravitacional está negativo porque o centro de massa G está descendo, ou seja, está havendo perda deste tipo de energia em relação ao referencial (.

Beleza!! Agora vamos substituir os valores:

Para uma barra, . Temos ainda que Logo:

Como (Não esquecer a regra da cadeira):

Para ângulos muito pequenos, vale a aproximação:

Portanto, substituindo e simplificando:

Arrumando a equação para o termo a segunda ficar com o coeficiente unitário, temos:

Agora temos uma equação nos moldes da equação do movimento harmônico. Com isto, sabemos a frequência natural:

A raiz deve dar um valor positivo para haver movimento harmônico simples. Então podemos estabelecer uma condição para k: