Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.5 - Ex. 119

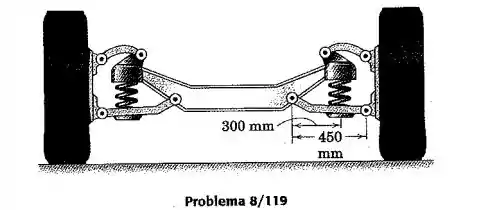
A suspensão dianteira de um automóvel é apresentada. Cada uma das molas helicoidais possui uma rigidez de 46.8 kN/m. Se a massa da extremidade dianteira do chassi e da parte equivalente da carroceria, presa à extremidade dianteira, é de 800 kg, determine a frequência natural f n da oscilação vertical do chassi e da carroceria na ausência de amortecedores. (Sugestão: Para relacionar a deflexão da mola ao deslocamento do chassi e da carroceria, considere o chassi fixo e assuma que o solo e as rodas se deslocam verticalmente.)

Passo 1

Para esse problema vamos utilizar as relações de conservação de energia como também uma relação para a deflexão vertical do sistema

Passo 2

Vamos começar considerando y o como a deflexão vertical do sistema. Temos que para a mola, a deflexão dela pode ser dada em termos da deflexão do sistema. Essa deflexão é dada por

300   m m 400   m m ⋅ y o = 2 3 ⋅ y o

Temos também que a variação da energia é dada por Δ E = Δ T + Δ U = 0 pois a energia será conservada. Temos que a única energia potencial que atua no sistema será a elástica e duas vezes maior por se tratar de duas molas, e a única cinética atuante será a translacional. Logo, temos que

Δ U = 2 ⋅ 1 2 ⋅ k ⋅ Δ y 2 = 2 ⋅ 1 2 ⋅ 46.8 k N m ⋅ 2 3 ⋅ y o 2 = 20.8 ⋅ y o 2   k J = 20800 ⋅ y o 2   J

Δ T = T m a x = 1 2 ⋅ m ⋅ y ˙ m á x 2 = 1 2 ⋅ 800   k g ⋅ y o 2 ⋅ ω n 2 = 400 ⋅ y o 2 ⋅ ω n 2   J

Igualando as duas equações agora, teremos que

400 ⋅ y o 2 ⋅ ω n 2   J = 20800 ⋅ y o 2   J

ω n = 20800 400   = 7.21   r a d / s

f n = ω n 2 ⋅ π = 7.21   r a d / s 2 ⋅ π = 1,148   H z

Resposta

f n = 1,148   H z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 15-51 mostra a posição de um bloco de 20 g oscilando em um MHS na extremidade de uma mola. A escala do eixo horizontal é definida por t s = 40,0 m s . Qual é (a) a energia cinética máxima do bl
Um bloco está em MHS na extremidade de uma mola, com a posição dada por x = x m c o s ω t + ϕ . Se ϕ = π / 5 r a d , que porcentagem da energia mecânica total é energia potencial no instante t = 0 ?
Um oscilador harmônico simples é formado por um bloco de 0,50 k g preso a uma mola. O bloco oscila em linha reta, de um lado para o outro, em uma superfície sem atrito, com o ponto de equilíbrio em x
Uma partícula de 3,0 k g está em movimento harmônico simples em uma dimensão e se move de acordo com a equação: x = 5,0c m c o s π 3rad / s t - π / 4 r a d com t em segundos. (a) Para que valor de x a
Um objeto fixado a uma mola descreve um Movimento Harmônico Simples com amplitude de 4,0 cm. Quando o objeto está a 2,0 cm da posição de equilíbrio, qual porcentagem da energia mecânica total está em