Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas - Ex. 104
Um objeto é colocado a uma distância de de uma tela. (a) Determine as posições dos dois pontos entre o objeto e a tela nos quais devemos colocar uma lente convergente com distância focal de para que se forme uma imagem sobre a tela. (b) Qual é a ampliação da imagem para cada uma dessas posições da lente?
Passo 1
(a) Bom, já que o objeto e a tela estão a um do outro, então essa relação aqui tem que ser verdade sempre:
Dá uma olhada no desenho pra entender melhor o porquê:
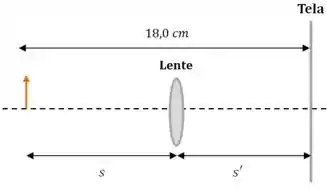
Passo 2
Beleza, vamos colocar isso na fórmula que descreve uma lente com distância focal e ver no que dá:
Multiplicando tudo por :
Agora é só resolver essa equação de segundo grau:
As duas soluções possíveis são e .
Isso quer dizer que a lente pode ser colocada ou à direita do objeto.
Passo 3
(b) Pra calcular a ampliação em cada um desses casos é só usar a fórmula:
Substituindo a nossa relação lá do passo 1:
Então para a ampliação é:
E para a ampliação é:
Resposta
(a) A lente pode ser colocada ou a à direita do objeto.
(b) A ampliação em cada um desses casos é e .