Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 28.Exercícios e Problemas - Ex. 45
Obtenha o campo elétrico interno e externo de uma bola de plástico com raio R e carga Q uniformemente distribuída sobre sua superfície.
Passo 1
Faaaaaala, galera... Tranquileba??
Sabendo que o campo para uma carga interna em uma superfície fechada é dada por:
E a área de uma esfera é dada por:
Passo 2
Desenhando a bola de plástico, temos:
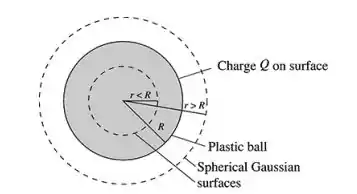
Onde temos a situação para campo em e
Passo 3
Para
Não há carga na superfície de logo . E portanto:
Para
Logo:
Resposta
Para
Para
Exercícios de Livros Relacionados
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui
Uma esfera sólida não condutora de raio R tem uma densidade volumétrica de arga que é proporcional à distância ao centro. Ou seja, ρ = A r para r ≤ R , onde A é uma constante. (a) Determine a carga to
Mostre que o campo elétrico devido a uma fina casca cilíndrica, infinitamente longa e uniformemente carregada, com raio a e densidade superficial de carga σ , é dado pelas seguintes expressões: E = 0
Uma esfera sólida não condutora de raio 1,00c m tem uma densidade volumétrica uniforme de carga. A magnitude do campo elétrico a 2,00c m do centro da esfera é 1,88 × 10 3N / C . (a) Qual é a densidade
Uma esfera de raio R em densidade volumétrica de carga ρ = C / r 2 para rR onde C é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões para o campo elét