Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.Problemas Adicionais - Ex. 93
Uma onda progressiva em uma corda é descrita pela equação
, onde e estão em centímetros e em segundos. (a)Para , plote em função de para . (b)Repita o item (a)para e para . A partir desses gráficos, determine (c)a velocidade da onda e (d)o sentido de propagação da onda.
Passo 1
(a)Beleza! Aqui, vamos substituir na equação da onda e gráfica-la, assim como fizemos em questões anteriores. Fazendo isso, a gente obtém:
Passo 2
(b) Para , temos:
Graficando essa equação, a gente obtém:
Agora, para , acontece que
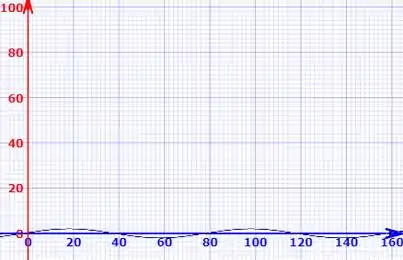
Passo 3
(c)Lembra da famosa equação da velocidade?
Ela também pode ser escrita assim:
Como podemos observar na equação da onda, (valor que multiplica . Além disso, também podemos ver que (valor que multiplica ). Dividindo esses dois valores, temos:
Passo 4
(d) Aqui, devemos lembrar que sempre que o sinal do fator que multiplica na equação da onda for positivo, isso significa que ela move-se no sentido negativo do eixo . Portanto, no caso da onda estudada aqui, podemos ver que ela move-se no sentido de
Resposta
(c)
(d)