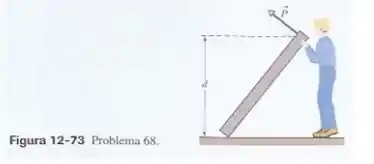
Um operário tenta levantar uma viga homogênea do chão até a posição vertical. A viga tem 2,50 m de comprimento e pesa 500 N. Em um certo instante, o operário mantém a viga momentaneamente em repouso com a extremidade superior a uma distância d=1,50 m do chão, como mostra a Fig. 12-73, exercendo uma força perpendicular à viga. (a) Qual é o módulo P da força? (b) Qual é o módulo da força (resultante) que o piso exerce sobre a viga? (c) Qual é o valor mínimo do coeficiente de atrito estático entre a viga e o chão para que a viga não escorregue nesse instante?

Como a viga está inclinada, podemos tirar um triângulo retângulo dali.

Pra achar o valor de P, basta a gente calcular os momentos com relação ao ponto de contato da viga com o solo.

Assim a gente já mata a letra (a).

Pra descobrir o valor da força resultante do piso sobre a viga, a gente faz o somatório das forças nas direções horizontal e vertical.

Como a gente já tem o valor de , então mole descobrir as componentes da reação. Fica e . O módulo da força resultante saí fácil.

Pra calcular o valor mínimo do coeficiente de atrito, a gente pode dividir sobre , e lembrar que atrito estático é igual força normal vezes o coeficiente de atrito estático.