A órbita da Terra em torno do Sol é quase circular: as distâncias de maior aproximação e maior afastamento são e , respectivamente. Determine as variações correspondentes (a) da energia total, (b) da energia potencial gravitacional, (c) da energia cinética e (d) da velocidade orbital. (Sugestão: use as leis de conservação da energia e do momento angular.)
Passo 1
Vamos começar ilustrando a situação:
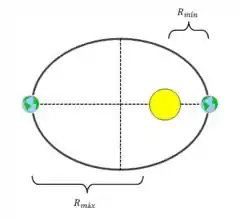
E a questão nos informou que e .
Passo 2
Beleza, a letra (a) quer a variação da energia total entre um ponto e outro. Essa é tranquila, porque a lei da conservação de energia diz que a energia total se conserva em um sistema fechado.
Como podemos pensar na Terra como um sistema fechado, podemos dizer que a variação da energia total é nula.
Passo 3
A letra (b) quer a variação da energia potencial gravitacional. Vamos lembrar que:
Portanto:
E essa é a resposta da letra (b).
Passo 4
A letra (c) quer a variação da energia cinética. Calcular cada uma das energias daria muito trabalho, porque ainda não temos as velocidades, então vamos usar a lei da conservação de energia.
Reorganizando isso:
Mas acabamos de calcular , ou seja:
Pronto!
Passo 5
A letra (d) pede a variação da velocidade orbital.
Aqui vamos aproveitar a dica do enunciado, e usar a lei de conservação do momento angular. Uma forma simples de escrever essa lei nesse caso é:
Cortando a massa da Terra:
Agora vamos aproveitar a variação da energia cinética que calculamos logo acima:
Podemos aproveitar isso para achar o valor de :
Passo 6
Agora vamos voltar à relação inicial que achamos entre e :
Substituindo:
E a diferença vai ser:
Pronto!
Resposta
(a)
(b)
(c)
(d)