Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.7 - Ex. 63

O tubo de Pitot (veja o problema 62) de um avião que está voando a grande altitude mede uma diferença de pressão de 180   P a . Qual é a velocidade do ar se a massa específica do ar nessa altitude é 0,031   k g / m 3 .

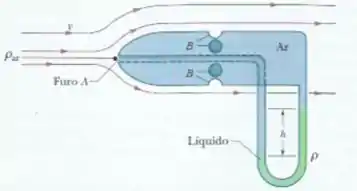
Figura do problema 62:

Passo 1

Show de bolinhas pessoal, uma das equações que demonstramos para a velocidade v no Exercício 62 é dada como:

v = 2 ρ g h ρ a r

Onde v é a velocidade do ar em relação ao avião, o ρ é a densidade daquele líquido verde, e ρ a r é densidade do ar.

Também no Exercicio 62, tínhamos demonstrado uma relação que vem da equação de Bernoulli aplicada ao tubo, dada como:

Δ p = p 1 - p 2 = ρ g h

Onde esse p 1 - p 2 é a diferença de pressão a que o enunciado se refere. Aí podemos colocar isso na equação de cima. Vai ficar assim ó:

v = 2 Δ p ρ a r

Passo 2

Iradoso, agora é só a gente substituir os valores da questão nessa fórmula, tal que:

v = 2 Δ p ρ a r

v = 2 180 0,031

v = 107,76

Logo:

v = 1,1 × 10 2   m/s

Resposta

A velocidade será v = 1,1 × 10 2   m/s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo horizontal se estreita de um diâmetro de 10 cm, na localização A, para um diâmetro de 5 cm, na localização B. Para um fluido incompressível e não-viscoso que escoa sem turbulência de A para B,
As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a á
Um pequeno orifício circular com diâmetro igual a 6,0mm é cortado na superfície lateral de um grande tanque de água , a uma profundidade de 14,0m abaixo da superfície da água, a uma profundidade de 14
Qual é a pressão manométrica necessária no tubo principal da rua para que uma mangueira de incendico ligada a ela seja capaz de lançar água até uma altura de 15,0m? (Suponha que o diâmetro do tubo pri
Uma bebida leve (essencialmente água) escoa em um tubo de uma fábrica de cerveja com uma vazão volumétrica tal que deve encher 220 latas de 0,355 L por minuto. Em um ponto do tubo, a pressão manométri