Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 62

Uma nave espacial encontra-se em uma órbita circular de raio r 0 em torno de um planeta de massa M. Um breve, porém intenso disparo de seu motor frontal diminui a velocidade da nave em 50%. Isso faz com que ela passe a descrever uma órbita elíptica. a. Qual é o valor da nova velocidade da espaçonave logo após o desligamento do foguete, em função de M, G e r 0 ? b. Em função de r 0 , qual é a distância mínima, e máxima, da espaçonave, em relação ao planeta, em sua nova órbita?

Passo 1

O esquema abaixo representa a situação descrita no enunciado.

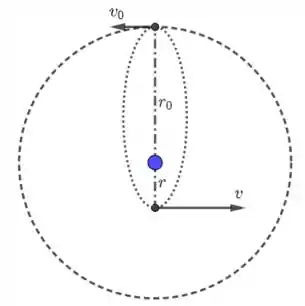
Inicialmente, a nave se encontra em uma trajetória circular de raio r 0 . Assim, a força gravitacional será uma componente centrípeta! Usando esse fato, poderemos calcular a velocidade v 0 .

Logo após a diminuição da velocidade da nave, ela passará a percorrer uma trajetória elíptica (como mostrado na figura), com o planeta sendo um dos focos da elipse. Note que a velocidade começa ao aumentar quando a nave vai se aproximando do planeta. Logo, o ponto onde ela estava inicialmente é o afélio (ponto da órbita elíptica mais afastado do planeta, que também é o ponto onde a nave possui a menor velocidade). O ponto de máxima aproximação, é o periélio. Podemos utilizar a conservação do momento angular entre o afélio e o periélio para escrever:

L a f é l i o = L p e r i é l i o m v 0 r 0 = m v r v 0 r 0 = v r

Essa última relação, juntamente com a conservação da energia mecânica, será muito útil na resolução do item b.

Passo 2

  1. Como dito no Passo 1, a força gravitacional será a componente centrípeta. Logo,

    2. m u 2 r 0 = G m M r 0 2 u = G M r 0

    Essa é a velocidade que a nave tinha na trajetória circular!! Pelo enunciado, temos que

    v 0 = 50 %   d e   u v 0 = 1 2 u v 0 = 1 2 G M r 0

    Passo 3

  2. A distância máxima, como vimos no Passo 1, é o próprio r 0 .

Para calcularmos a distância mínima, temos:

  • v 0 r 0 = v r ∴ v = v 0 r 0 / r ;
  • Conservação da energia:

K a f é l i o + U a f é l i o = K p e r i é l i o + U p e r i é l i o 1 2 m v 0 2 - G m M r 0 = 1 2 m v 2 - G m M r G M r - G M r 0 = 1 2 v 2 - v 0 2 G M 1 r - 1 r 0 = 1 2 v 0 2 r 0 2 r 2 - v 0 2 G M r 0 - r r r 0 = 1 2 v 0 2 r 0 2 - r 2 r 2 G M r 0 - r r 0 = 1 2 v 0 2 r 0 - r r 0 + r r G M r 0 = 1 2 v 0 2 ⋅ r 0 + r r

Substituindo o valor de v 0 , temos

G M r 0 = 1 2 1 4 ⋅ G M r 0 ⋅ r 0 + r r 8 = r 0 + r r 8 r = r 0 + r 7 r = r 0 r = r 0 7

Portanto, a distância mínima valerá r 0 / 7 .

Resposta

  1. 1 2 G M r 0 .
  2. r 0 7 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cometa que foi visto em abril de 1574 por astrônomos chineses, em um dia conhecido como Woo Woo, foi avistado novamente em maio de 1994. Suponha que o intervalo de tempo entre as observações seja o
O Sol, que está a 2,2.10 20m do centro da Via Láctea, completa uma revolução em torno do centro a cada 2,5.10 8 anos. Supondo que todas as estrelas da galáxia possuem uma massa igual à massa do Sol, 2
O centro do Sol está em um dos focos da órbita da Terra. A que distância desse foco se encontra o outro foco (a) em metros e (b) em termos do raio solar, 6,96.10 8m ? A excentricidade da órbita da Ter
Um satélite de 20k g está em uma órbita circular com um período de 2,4h e um raio de 8,0.10 6m em torno de um planeta de massa desconhecida. Se o módulo da aceleração gravitacional na superfície do pl
Em um certo sistema estelar binário, as duas estrelas têm uma massa igual à do Sol e giram em torno do centro de massa. A distância entre as estrelas é igual à distância entre a Terra e o Sol. Qual é,