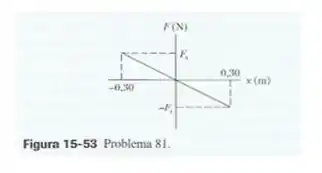
Um oscilador harmônico simples é formado por um bloco de preso a uma mola. O bloco oscila em linha reta, de um lado para o outro, em uma superfície sem atrito, com o ponto de equilíbrio em . No instante , bloco está em e se move no sentido positivo de . A Fig. 15-53 mostra o módulo da força aplica em função da posição do bloco. A escala vertical é definida por . Qual é (a) a amplitude do movimento, (b) o período do movimento, (c) o módulo da aceleração máxima e (d) a energia cinética máxima.

Antes de acharmos o período, vamos precisar do valor da constante elástica da mola. Pra isso, usaremos a lei de Hooke:

Onde é a inclinação (negativa) do gráfico, e vale:

Sabendo disto, vamos usar a equação do período de um oscilador harmônico simples para encontrar o período, dada como:

Sendo assim, vamos ter que:

Para achar a aceleração máxima, a gente só precisa substituir os valores da frequência angular e amplitude do movimento na equação abaixo

Sendo assim:

Iradoso galerinha, sabendo da velocidade máxima, a gente consegue chegar na energia cinética máxima do movimento. Vamos usar a relação abaixo para descobrir a velocidade máxima:

Substituindo esta equação na equação da energia cinética, a gente obtemos:

Portanto, substituindo os valores que enunciado nos fornece: