Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 14.Exercícios e Problemas - Ex. 9
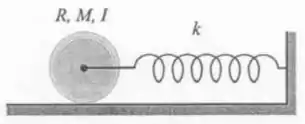
. (Repetição de problema do Capítulo , Oscilador harmônico.) Ao oscilar forçado pela mola, o cilindro visto na figura rola sobre o piso, girando livremente em torno do seu eixo. Escreva a lagrangeana do sistema. Calcule a frequência natural do oscilador. (Observe como a solução é mais simples pelo método de Lagrange.)
Passo 1
Vem comigo que a gente detona essa questão!
Para escrever a Lagrangeana do sistema temos que saber a energia cinética e potencial desse sistema, já que:
Para descrever o problema vamos usar a coordenada generalizada , que é a distância do centro de massa do cilindro em relação ao ponto onde a mola está presa, já que só com ela conseguimos descrever a posição do cilindro.
Como o cilindro descreve um movimento de translação do centro de massa e de rotação ao mesmo tempo, temos que a energia cinética seguinte forma:
Nesse caso só temos a energia potencial elástica da mola, que é da seguinte forma:
Onde é o quanto a mola foi deformada, então temos que escrever essas equações em termos da nossa coordena generalizada .
Para achar a frequência de oscilação desse pêndulo, teremos que escrever a equação de Lagrange para a coordenada e analisar o que temos, a equação de Lagrange é da seguinte forma:
Vamos ao trabalho!
Passo 2
Primeiro vamos mexer com a energia cinética, temos o seguinte:
Em um movimento de rotação temos que , assim temos:
Lembrando que , temos:
Passo 3
Agora vamos mexer com a energia potencial, temos o seguinte:
Onde esse acaba sendo igual a posição do cilindro menos o comprimento natural da mola, assim:
Então a Lagrangena fica da seguinte forma:
Passo 4
Agora vamos escrever a equação de Lagrange para . Vamos calcular cada parte da equação separadamente depois juntamos tudo.
Primeiro vamos calcular , temos:
Agora vamos calcular , então:
Agora por último , temos:
Juntando tudo temos:
Passo 5
Vamos mexer um pouco nessa equação que encontramos.
Essa equação se parece com a equação do oscilador harmônico, então temos que a frequência angular é dada por:
E usando que , temos que a frequência de oscilação é:
E com isso terminamos essa questão!