Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.2 - Ex. 37
Uma mola de massa desprezível está pendurada no teto com um pequeno objeto preso à extremidade inferior. O objeto é inicialmente mantido em repouso em uma posição , tal que a mola se encontra no estado relaxado. Em seguida, o objeto é liberado e passa a oscilar para cima e para baixo, com a posição mais baixa abaixo de . (a) Qual é a frequência das oscilações? (b) Qual é a velocidade do objeto quando se encontra abaixo da posição inicial? (c) Um objeto de massa é preso ao primeiro objeto, após o que o sistema passa a oscilar com metade da frequência original. Qual é a massa do primeiro objeto? (d) A que distância abaixo de está a nova posição de equilíbrio (repouso), com os dois objetos presos à mola?
Passo 1
Pra gente entender a física do problema, a figura abaixo mostra um esquema do problema. O objeto entra em equilíbrio quando a força da gravidade (que aponta para baixo) é balanceada com a força da mola (apontada para cima).
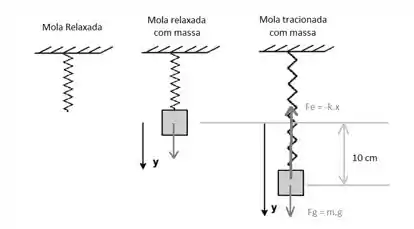
Vamos chamar de a variação do comprimento da mola entre seu ponto relaxado e seu ponto de equilíbrio.
Assim, fazendo o balanço das forças na condição de equilíbrio, a gente tem:
Onde é a constante da mola e é a massa1 do objeto. Então:
Sabendo da razão , a gente consegue calcular a frequência de oscilação
Passo 2
Para responder este item, usaremos a conservação da energia mecânica. Adotaremos o zero da energia potencial gravitacional no ponto inicial do objeto, que é o ponto onde a mola está relaxada. Neste ponto, a energia potencial e a energia cinética são zero, logo a energia mecânica será zero (). O eixo será positivo para baixo e . A energia potencial quando o objeto está nesse ponto é
A equação da conservação de energia mecânica fica:
Agora, basta isolar a velocidade na equação acima e encontrar o seu valor:
Passo 3
Sendo a massa original e a massa adicional, a nova frequência angular é
Como a nova frequência deve ser a metade da frequência original, a gente tem que
Igualando as equações:
Substituindo valores do problema, temos:
Passo 4
A nova posição de equilíbrio é determinada pelo balanceamento entre a força da gravidade e a força da mola, da mesma forma que a gente fez no item (a)
Antes de resolver essa equação, a gente precisa achar o valor da constante da mola . Como a gente já sabe a massa e a frequência de oscilação do sistema sem a adição de massa, a gente pode calcular dessa forma:
Então
Lembrando que esse valor é medido a partir do ponto inicial, que o ponto onde a mola encontra-se relaxada.
Resposta
(a)
(b)
(c)
(d)