Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 37.Problemas adicionais - Ex. 65

Outra abordagem para as transformações de velocidades. Na Fig. 37-31, os referenciais B e C se movem em relação ao referencial A na direção comum dos eixos x . Podemos representar os componentes x das velocidades de um referencial em relação a outro através de um índice duplo. Assim, por exemplo, v A B é a componente x da velocidade de A em relação a B . Os parâmetros de velocidades podem ser representados da mesma forma: β A B = v A B c   , por exemplo, é o parâmetro de velocidade correspondente a v A B . (a) Mostre que

β A C = β A B + β B C 1 + β A B ⋅ β B C

Seja M A B a razão 1 - β A B 1 + β A B e sejam M B C e M A C razões análogas. (b) Mostre que a relação

M A C = M A B ⋅ M B C

É verdadeira demonstrando a partir desta relação a equação do item (a)

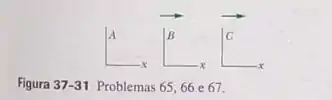
Passo 1

Para resolvermos esse problema vamos utilizar a Eq. 37-29 e muitas manipulações algébricas para encontrarmos as equações pedidas pelo enunciado.

Passo 2

  1. Vamos começar chorando um pouco.... Pronto! Agora podemos começar. Vamos utilizar a equação 37-29 de uma maneira um pouco diferente. Iremos escreve-la da forma

    2. V A C = V A B + V B C 1 + V A B ⋅ V B C c 2

    Se multiplicarmos em cima e em baixo por c , teremos que

    V A C = V A B + V B C ⋅ c 1 + V A B ⋅ V B C c 2 ⋅ c

    E como β = V c , ficamos com

    β A C = β A B + β B C 1 + β A B ⋅ β B C

    Passo 3

  2. Vamos partir da relação dada no enunciado, onde M = 1 - β 1 + β , temos que

M A C = M A B ⋅ M B C → 1 - β A C 1 + β A C = 1 - β A B 1 + β A B ⋅ 1 - β B C 1 + β B C

Eliminando os termos no denominador, temos que

1 + β A C ⋅ 1 - β A C ⋅ 1 + β B C = 1 - β A B ⋅ 1 - β B C ⋅ 1 + β A C

Fazendo a distributiva e eliminando os termos que aparecem dos dois lados da equaçã0, chegamos que

- β A C + β A B + β B C - β A B ⋅ β B C ⋅ β A C = β A C - β A B + β A B ⋅ β B C ⋅ β A C

2 ⋅ β A B + 2 ⋅ β B C = 2 ⋅ β A C + 2 ⋅ β A B ⋅ β B C ⋅ β A C

Colocando termos em evidencia, vemos que

2 ⋅ β A B + β B C = 2 ⋅ β A C ⋅ 1 + β A B ⋅ β B C

β A C = β A B + β B C 1 + β A B ⋅ β B C

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para girar em volta da Terra em uma órbita de baixa altitude, um satélite deve ter uma velocidade de aproximadamente 2,7 × 10 4k m / h . Suponha que dois satélites nesse tipo de órbita giram em tomo d
Um cruzador dos forons, que está na rota de colisão com um caça dos reptulianos, dispara um míssil na direção da outra nave. A velocidade de míssil é 0,980 c em relação à nave dos reptulianos e a velo
Uma partícula de massa m tem uma velocidade de c 2 em relação ao referencial inercial S. A partícula colide com uma partícula igual em repouso no referencial. Qual a velocidade, em relação a S, de um
A galáxia A está se afastando da Terra com uma velocidade de 0,35c. A galáxia B, situada na direção diametralmente oposta, está se afastando de nós com a mesma velocidade. Que múltiplo de c correspond
O referencial S’está se movendo em relação ao referencial S com uma velocidade de 0,62c i → enquanto uma partícula se move paralelamente aos eixos coincidentes x e x’. Para um observador estacionário