Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 7.Problemas - Ex. 14

Utilize o Princípio dos trabalhos Virtuais enunciado na Seç. 7.3 para obter as condições de equilíbrio da alavanca[ Fig . a)] e do plano inclinado [Fig. b)]. Para isto, imagine que um pequeno deslocamento, compatível com os vínculos a que estão sujeitas, é dado às massas, e imponha a condição de que o trabalho realizado nesse deslocamento (trabalho virtual) deve ser nulo.

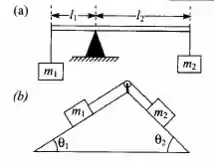
Passo 1

  1. Nesse primeiro caso a gente só precisa imaginar o que aconteceria se deslocássemos um pouquinho de nada algumas das massas pra baixo ou pra cima. Bom, como as forças de tração não realizam trabalho sobre o sistema porque são forças de vínculo temos que o trabalho resultante é dado por

    2.           d W t o t a l = d W g 1 + d W g 2

    Aqui enquanto a gravidade realiza um trabalho positivo em um corpo, realiza um negativo sobre o outro. Por isso a gente tem

    d W t o t a l =   m 1 g d x 1 - m 2 g d x 2 = 0

    →

    m 1 d x 1 = m 2 d x 2

    Mas e agora? Como saber quem é d x 1   e   d x 2 ? Calma, vem comigo!

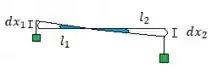
    Nosso ângulo azul representa o deslocamento angular de cada bloquinho, ele tem que ser o mesmo pela simetria do problema, beleza? Mas a gente sabe também que nossas distâncias verticais d x 2   e   d x 1 são iguais aos arcos percorridos pelos bloquinhos quando se trata de dimensões infinitesimais. Então

    d x 2 = l 2 θ

    d x 1 = l 1 θ

    →

    m 1 l 1 θ = m 2 l 2 θ

    →

    m 1 l 1 = m 2 l 2

    Passo 2

  2. Aqui vamos usar a mesma lógica

d W g = 0  

→

P 1 d x 1 = P 2 d x 2

→

m 1 g s e n θ 1 d x 1 = m 2 g s e n θ 2 d x 2

Mas aqui temos d x 1 = d x 2 , já que estão conectados pelo cabo, por isso

m 1 s e n θ 1 = m 2 s e n θ 2

Bora treinar mais?

Resposta

a )   m 1 l 1 = m 2 l 2

b )   m 1 s e n θ 1 = m 2 s e n θ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura abaixo mostra a força F x que atua sobre urna partícula de 0,500 kg. (a) Do gráfico, calcule o trabalho realizado pela força enquanto a partícula se move de x = 0,00 até os seguintes valores
Uma forca F → = 2,0N x 2 i ^ é aplicada sobre uma partícula inicialmente em repouso no plano xy. Encontre o trabalho realizado por esta força sobre a partícula e a rapidez final da partícula, quando e
Uma força atuando sobre uma partícula de 2,0 kg do plano xy, nas coordenadas (x, y), é dada por F → = - b / r 3 x i ^ + y j ^ , onde b é uma constante positiva e r é a distância da partícula à origem.
Uma força horizontal única, com a orientação de +x, atua sobre um carrinho de massa m. O carrinho parte do repouso em x = 0, e sua rapidez cresce com x como v = Cx, onde C é uma constante. (a) Encontr
Uma força atuando sobre uma partícula do plano xy, nas coordenadas (x, y), é dada por F → = F 0 r y i ^ - x j ^ onde F 0 é uma constante positiva e r é a distância dapartícula à origem. (a) Mostre que