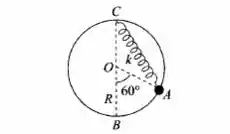
Um corpo de massa m= 300g , enfiado num aro circular de raio R= 1m situado num plano vertical, está preso por uma mola de constante elástica k = 200 N/m ao ponto C, no topo do aro (Fig.). Na posição relaxada da mola, o corpo está em B, no ponto mais baixo do aro. Se soltarmos o corpo em repouso a partir do ponto A indicado na figura, com que velocidade chegará a B?

Se usarmos leis de Newton aqui vai dar um trabalhão né galera? Vamos apelar para o teorema trablho – energia cinética. Para descobrir nosso trabalho resultante vamos apelar para quem? Haha, nossa energia potencial! Vem comigo!

(Já que todas as forças atuantes são conservativas)

Vamos primeiro considerar a energia potencial de B como nula para facilitar as coisas, e é até mesmo natural que seja assim, já que B é o ponto mais baixo da trajetória e a posição de equilíbrio da mola, beleza?

A energia no ponto A é dada por

Nossa missão agora é achar esses valores, vamos fazer um esqueminha pra ver como fica

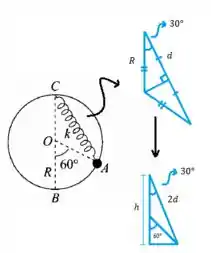
Podemos perceber que o triângulo de cima, onde o lado maior é a mola, é isósceles e por isso tem seus ângulos laterais são de , já que o central é . Dito isso, a gente pode calcular aquela distância , que é metade do comprimento da mola no ponto A. Fica asism

Daqui a gente já sabe de quanto foi a deformação da mola, certo? Se no equilíbrio seu comprimento é

Agora pra saber o quanto o corpo está acima do ponto B, basta fazermos . Pelo nosso esquema temos

Então nossa altura fica