Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 6.1 - Ex. 4
Suponha que o trabalhador do Exercício empurre o engradado para baixo de um plano inclinado de abaixo da horizontal.
a) Qual é o módulo da força aplicada pelo trabalhador para que o engradado se desloque com velocidade constante?
b) Qual é o trabalho realizado por essa força sobre o engradado quando ele se desloca de ?
c) Qual é o trabalho realizado pelo atrito sobre o engradado durante esse deslocamento?
d) Qual é o trabalho realizado sobre o engradado pela força normal? E pela força da gravidade?
e) Qual é o trabalho total realizado sobre o engradado?
Passo 1
Nesse problema temos uma pessoa empurrando um engradado de pra baixo por em um plano de . Temos que:
Que é o atrito cinético entre o piso e o engradado. A gente deve responder qual é o módulo da força aplicada pelo trabalhador para que a velocidade de deslocamento seja constante!
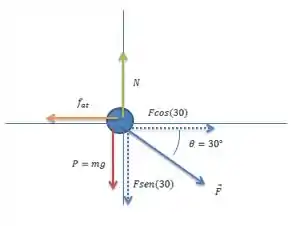
O desenho das forças fica assim:
Já separei as componentes vertical e horizontal da força . A caixa se movimenta com velocidade constante, então a soma das forças numa mesma direção é zero. Assim, ficamos com um sistema de equações. Na vertical:
E na horizontal:
Mas sabemos que a força de atrito depende da normal, então vamos substituir a expressão de na força de atrito:
A massa do engradado é , o coeficiente de atrito cinético é a gravidade já estamos carecas de saber que vale , então agora é só substituir os valores e achar o valor de :
Passo 2
O trabalho da força vai ser:
Passo 3
O trabalho da força de atrito vai ser igual ao trabalho da componente horizontal da , mas com sinal oposto. Mas não basta dizer, precisamos encontrar esse valor, não é verdade? Então vamos começar calculando a força de atrito. Do passo temos uma expressão pra ela:
Como temos todos os valores de massa, força e coeficiente de atrito, é só substituir:
E agora podemos calcular o trabalho, lembrando que a força de atrito é oposta ao deslocamento, então :
Passo 4
O deslocamento é na horizontal, e apenas as forças que estejam nessa direção (ou tenha componentes nessa direção) é que vão realizar trabalho. E isso não é o caso nem da força peso nem da força normal. Ambas as forças estão apenas na direção vertical, e não possuem componentes na horizontal, por isso não realizam trabalho.
Outra forma de ver isso é identificando o ângulo entre a força e o deslocamento. Tanto a força normal quanto a força peso fazem um ângulo de com o deslocamento, assim o trabalho é zero, pois :
Passo 5
O trabalho total é a soma dos trabalhos de cada força:
Como , e os outros valores calculamos nos itens e é só substituir:
Assim o trabalho total é zero!
A força resultante sobre o engradado é zero, logo o trabalho total realizado sobre ele também deve ser zero.