Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 6.Problemas - Ex. 62
Um pacote de desliza para baixo de uma rampa inclinada de a abaixo da horizontal. O coeficiente de atrito cinético entre o pacote e a rampa é . Calcule
a) o trabalho realizado sobre o pacote pelo atrito;
b) o trabalho realizado sobre o pacote pela gravidade;
c) o trabalho realizado sobre o pacote pela força normal;
d) o trabalho total realizado sobre o pacote.
e) Se o pacote possui uma velocidade de no topo da rampa, qual é sua velocidade depois de descer ao longo da rampa?
Passo 1
Opa, bora resolver esse problema! Temos um pacote deslizando uma rampa conforme o esquema abaixo:
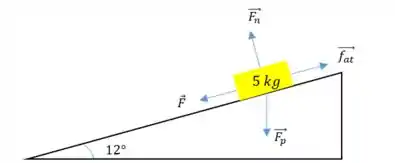
O enunciado diz que o coeficiente de atrito cinético entre o pacote e a rampa é . Sabendo disso, a primeira coisa que precisamos calcular é o trabalho realizado sobre o pacote pelo atrito.
Bora lá! Podemos calcular o trabalho do pacote sobre o atrito fazendo:
Esse sinal negativo é porque a força de atrito é oposta ao movimento. Ela pode ser calculada por:
Ou seja:
Calculando:
Passo 2
Agora queremos o trabalho realizado sobre o pacote pela gravidade! Temos que:
Substituindo a força peso:
O ângulo entre a força peso e o deslocamento é , assim o trabalho da força peso é:
Passo 3
Vamos calcular o trabalho realizado sobre o pacote pela força normal!
O ângulo entre a força normal e o deslocamento é como não precisamos nem nos dá o trabalho de calcular!
Passo 4
Tá quase acabando! O trabalho total é a soma dos trabalhos:
Passo 5
Agora pra acabar, vamos usar o teorema trabalho – energia. A velocidade inicial é e queremos saber a velocidade final . O trabalho total já calculamos, agora é só aplicar isso no teorema:
Temos que:
Então:
Tranquilo? Vamos pra próxima?