84. Um motociclista audacioso deseja estabelecer um recorde saltando sobre ônibus escolares em chamas. Ele vem pedir a você para ajudá-lo no planejamento. Ele pretende decolar de uma plataforma horizontal a , atravessar voando os ônibus em chamas posicionados dentro de uma depressão no solo e aterrissar sobre outra rampa inclinada para baixo em . É muito importante que a moto não ricocheteie ao atingir a rampa de aterrissagem, pois isso poderia fazê-lo perder o controle e cair. Você logo percebe que ele evitará o ricocheteio se sua velocidade ao final do salto for paralela à rampa de aterrissagem. Isso pode ser conseguido se a rampa for tangente à trajetória da moto e se ele aterrissar à direita da borda da rampa de aterrissagem. Não existe lugar para erro! Sua tarefa é determinar onde posicionar a rampa de aterrissagem, ou seja, a que distância horizontal da extremidade da plataforma de lançamento deve estar a parte frontal da rampa de aterrissagem e qual é a diferença de altura apropriada entre as bordas dessas duas estruturas? Em seu contrato existe uma cláusula que exige que você teste o projeto antes que o “herói” vá ao ar em rede nacional de televisão para tentar estabelecer seu recorde.
Passo 1
Tudo bem senhores!? Aqui vamos nós de novo pra mais uma questãozinha de Cinemática!
E pra resolver esse tipo de questão, já sabe né?
Como é de costume; primeiramente bora fazer um esboço pra ajudar a entender melhor o nosso problema...
De modo que obtemos então, a seguinte imagem abaixo...
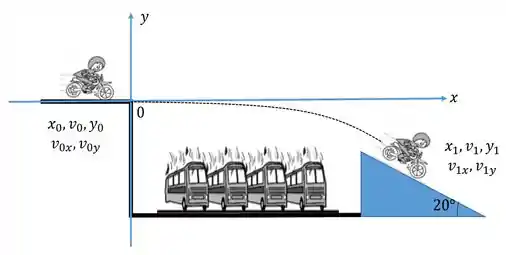
Sendo que a imagem acima retrata o que a gente quer que aconteça, né!? Afinal; coitado do motociclista se ele se estabacar no meio daqueles ônibus!
E pelo que sabemos dos problemas de lançamento horizontal e movimento oblíquo e também do que lemos no enunciado, tiramos que...
Onde o objetivo aqui é encontrar onde devemos posicionar a rampa para que o salto do nosso maluco seja perfeito... No caso precisamos de e !
Por isso, mãos à obra!
Passo 2
Bora pro que interessa! Chega de introdução!
Tomando como o instante inicial do movimento do skatista... Pra facilitar a nossa resolução, bora dividir o movimento do motoqueiro depois que sai da plataforma horizontal, em duas partes; vertical e horizontal...
Na horizontal, em , nosso camarada não tem aceleração influenciando seu movimento. Sendo assim, ele executa um movimento uniforme, com velocidade constante.
Olhando pra nossa figura do , ficamos então com...
E substituindo os valores numéricos de cada variável;
Obtemos a equação que descreve a trajetória do nosso amigo segundo a direção ...
Passo 3
Indo agora pra direção vertical, temos nessa direção a presença da aceleração da gravidade para baixo influenciando a trajetória do nosso motoqueiro.
Desse modo, peguemos a equação abaixo da posição para o movimento uniformemente variado... É claro, usando as variáveis da nossa figura, né!?
Esse é a nossa aceleração da gravidade , com sinal negativo porque aponta para baixo...
Ficamos então, com...
Logo; substituindo os valores conhecidos...
Obtemos a equação que descreve o movimento vertical!
E agora é so ir atrás do tempo !
Passo 4
Bora seguir em frente!
Bom! Pela figura do , podemos ver que o objetivo é que o motociclista aterrisse na rampa... Só que essa rampa faz um ângulo de com o sentido horário!
Logo, quando ele aterrissa na rampa em , a seguinte relação abaixo entre as velocidade é válida...
Se sentiu dúvida aí porque o ângulo tá negativo, é devido ao fato de que ele é obtido através da rotação em sentido horário com a horizontal... Geralmente adota-se a convenção hoária como negativa e anti-horária como positiva.
Se tá tudo ok; uma vez que a velocidade horizontal é constante ao longo de todo o movimento do nosso amigo, então...
E desse modo, o valor de é dado por...
Com isso, vamos recorrer a equação da velocidade em para o movimento uniformemente variado. De acordo com os dados do nosso problema, chegamos à seguinte equação...
E como queremos o tempo então bora logo substituir os valores de cada variável...
Passo 5
Obtido o tempo total do movimento do skatista desde que ele sai rampa; para obter as posições onde a rampa deve estar, basta substituir o nas equações de movimento obtidas anteriormente...
Para o eixo :
E depois, para o eixo :
Pronto! Essas são as posições onde no mínimo, a rampa deve estar!
Terminamos aqui! Até a próxima!