Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.3 - Ex. 14
Uma bola de gude rola horizontalmente com velocidade escalar e cai do topo de uma
plataforma de 2,75m de altura, sem sofrer nenhuma resistência significativa do ar.
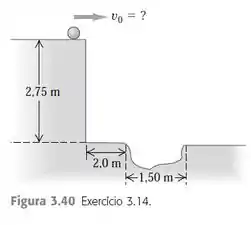
No nível do solo, a 2,0m da base da plataforma, há um buraco escancarado (Figura 3.40). Para qual alcance da velocidade a bola de gude aterrissará no buraco?
Passo 1
E aí, galerinha!
Nesse problema temos uma bolinha de gude que possui uma velocidade horizontal . Ela se encontra a uma altura de e ao cair, a bolinha aterrissa em um buraco de de comprimento que está a de onde a bolinha salta.
A partir daí queremos saber qual é a velocidade máxima e mínima da bolinha para que ela caia no buraco...
Parece complicado?
A bolinha de gude se move com movimento de projétil, com velocidade inicial horizontal .
Se for muito pequeno, a bola de gude pousará na esquerda do buraco e se for muito grande, a bolinha de gude caira a direita do buraco.
Em , vamos tomar para a direita sendo positivo, com:
Em , vamos tomar para cima como positivo, com:
Veja só!
Passo 2
Nós vamos usar o movimento vertical, , para encontrar o temoi, , que a bola de gude leva para atingir a altura do nível do solo, a partir da seguinte equação:
Sabemos que , . E Então:
O tempo não depende da velocidade .
Passo 3
Agora precisamos calcular a velocidade máxima e a velocidade mínima:
Quando mínima:
Quando máxima:
Nós utilizaremos a equação:
E para ambas o tempo, , nós encontramos acima:
Tranquilo até aqui?
Passo 4
Dessa forma,
Estamos quase lá!
Passo 5
E por ultimo...
O que achou? Responde Aí! 😁
