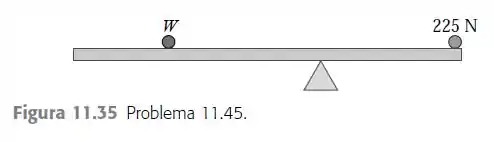
Uma barra uniforme de e de comprimento carrega um peso de na extremidade direita e um peso desconhecido em direção à extremidade esquerda (Figura ). Se é colocado a da extremidade esquerda da barra, o sistemase equilibra horizontalmente quando o sustentáculo está localizado a da extremidade direita. a) Ache . b) Se for movido para a direita, qual distância e em que direção o sustentáculo deve ser deslocado para restabelecer o equilíbrio?

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente determinar o valor do peso na direção da extremidade esquerda da barra, sabendo que ele é colocado a dessa extremidade e que o sistema se equilibra horizontalmente quando o sustentáculo está localizado a da extremidade direita. Depois, precisamos ver o que acontece quando o peso é movido para a direita.

A figura mostra exatamente o que o enunciado descreveu, mas temos que nos ligar que esse , na verdade é o peso colocado sobre a barra.

E o bizu aqui, é que em cada caso, para alcançar o equilíbrio, o centro de gravidade do sistema deve estar no ponto de apoio.

Vamos usar a seguinte equação para localizar o centro de massa:

Substituindo por .

Vamos considerar a origem na extremidade esquerda da haste e pegar o eixo ao longo da haste. Assim, teremos que:

da haste

Como ela é uniforme e o seu centro de massa está no meio dela, então . Sendo assim, sabendo que o peso na extremidade tem , então vamos ter . E para o terceiro peso, que vamos chamar de , teremos:

Como descrito no enunciado. Agora vamos aplicar isso na equação do centro de massa!

Vamos lá!