Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 77
Uma mola está em pé sobre uma mesa, com sua extremidade inferior fixada à mesa. Um bloco é solto de uma altura de e cai sobre a extremidade superior da mola. Ele fica preso à extremidade superior da mola e, então, oscila com amplitude de 10 cm. Qual é a frequência de oscilação?
Passo 1
Se liga! Na imagem a seguir, a posição A indica a posição inicial do bloco, B é o ponto em que o bloco entra em contato com a mola, C indica quando o sistema está na posição de equilíbrio e D a máxima compressão da mola.
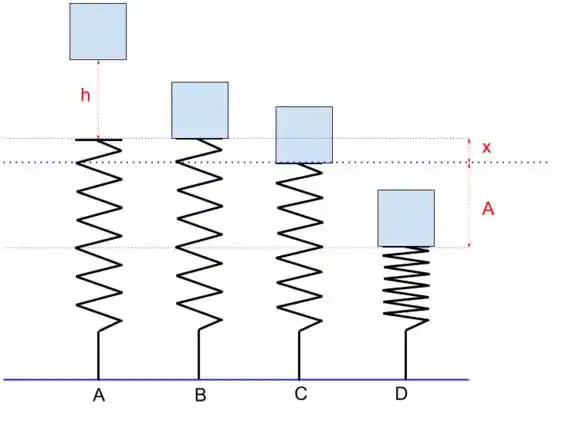
Precisamos observar que a oscilação ocorrerá em torno do ponto de equilíbrio. Neste caso, o ponto de equilíbrio é quando a força peso se anula com a força elástica. Então podemos escrever que
Esta expressão nos dá a informação do deslocamento do ponto de equilíbrio em relação a posição relaxada da mola.
Passo 2
Como queremos descobrir a frequência de oscilação, precisamos nos lembrar que
Pela equação (1) podemos reescrever
Passo 3
Agora podemos usar a conservação da energia.
Tomando a posição de equilíbrio como podemos dizer que em A a energia do sistema é
Em B a energia do sistema é
Onde
Logo
Em C a energia do sistema é
Onde
Logo
Em D a energia do sistema é
Onde
Logo
Passo 4
Se igualarmos a equação (5) com (7), teremos
Podemos escrever em função da altura que o objeto cai, ou seja, usaremos Torricelli.
Substituindo na equação (8), temos
Usando a equação (1) e substituindo , temos
Agora podemos eliminar que aparece em todas as parcelas
Passo 5
Se reescrevermos a equação (10), temos
Repare que conhecemos os valores de e , pois foram dados no enunciado. Sendo assim, temos uma equação de segundo grau e precisamos encontrar o valor de . Substituindo os valores conhecidos temos
Resolvendo a equação acima encontramos os valores de
Como no referencial usado sabemos que , então ficaremos com
Passo 6
Como queremos achar a frequência, precisamos retornar para a equação (3). Portanto
Substituindo este valor na equação (2), temos