Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 6.Problemas - Ex. 3
Uma partícula de massa m= 1Kg, lançada sobre um trilho retilíneo com velocidade 3 m/s, está sujeita a uma força F(x) = -a -bx, onde a= 4N, b = 1 N/m e x é o deslocamento, em m, a partir da posição inicial. a) Em que pontos do trilho a velocidade da partícula se anula? b) Faça o gráfico da velocidade da partícula entre esses pontos. c) A que tipo de lei de forças corresponde F(x) ?
Passo 1
(a) Para que a velocidade da partícula se anule é necessário que sua energia cinética varie em , logo o trabalho que essa força realiza em um deslocamento de x’ metros sobre a partícula deve ter esse mesmo valor:
Substituindo os valores:
Resolvendo a integral,
Reorganizando temos
Finalmente,
Logo nossa velocidade é igual a 0 em
Passo 2
(b) Para descobrir a velocidade em função de x, vamos usar a mesma relação anterior. Sabendo que a massa é de 1kg e a velocidade inicial 3 m/s temos,
Integramos em relação a x’, só porque a variável não pode ser igual ao limite de integração! Só um detalhe matemático, mas que não vai fazer diferença, tá? Integrando:
Colocando a nossa velocidade em evidência:
Para descobrir a velocidade tomamos a raíz quadrada em ambos os lados
Portanto, o gráfico da nossa partícula fica assim
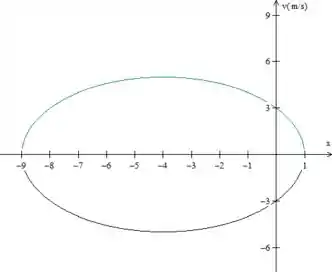
Isso acontece porque nossa partícula pode ter velocidade negativa ou positiva para uma mesma posição x, a depender se ela está indo ou voltando, como uma mola.
Passo 3
(c) Essa força atua como a força elástica onde seu ponto de equilíbrio ocorre quando