Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 6.Problemas - Ex. 43
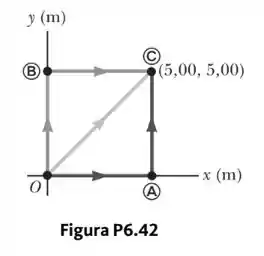
Uma força que age sobre uma partícula que se move sobre o plano é determinada por , em que está em newtons e e estão em metros. A partícula se move da origem à sua posição final com coordenadas e , como mostrado na Figura P6.42. Calcule o trabalho realizado por sobre a partícula enquanto ela se move
pelo caminho mais escuro,
pelo caminho cinza escuro e
pelo caminho cinza claro.
é conservativa ou não conservativa?
Explique sua resposta à parte (d).
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer mais uma questãozinha aqui?
Vem comigo!
Nas seguintes integrais, lembre-se de que:
Letra a:
O trabalho feito na partícula em sua primeira seção de movimento é:
e já que ao longo deste caminho,
Na próxima parte de seu caminho:
Para
Passo 2
Letra b:
Seguindo as mesmas etapas,
já que ao longo deste caminho,
Como :
Passo 3
Letra c:
Já que x = y em OC:
Passo 4
Letra d:
F é não conservativo.
Passo 5
Letra e:
O trabalho feito na partícula depende do caminho seguido pela partícula.
Resposta
- F é não conservativo.
- O trabalho feito na partícula depende do caminho seguido pela partícula.