Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 6.Problemas - Ex. 7
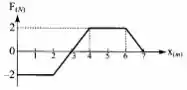
Uma partícula de massa m=2Kg desloca-se ao longo de uma reta. Entre x=0 e x=7 m, ela está sujeita à força F(x) representada no gráfico. Calcule a velocidade da partícula depois de percorrer 2,3,4,6 e 7 m, sabendo que sua velocidade para x=0 é de 3 m/s.
Passo 1
Usando o teorema do Trabalho-Energia cinética fica assim
Vamos avaliar o trabalho realizado entre ,
Só que calcular essa integral, é simplesmente calcular a área embaixo do gráfico. E pela área embaixo do gráfico concluímos que
Sempre vamos calcular a área embaixo do gráfico para achar a integral,fechou? Então a partir de agora vamos escrever
Passo 2
Para o percurso de 3m:
Vamos calcular a área do trapézio que aparece entre 0 e 3:
Passo 3
Para o percurso de 4m:
Vamos calcular a área do trapézio que aparece entre 0 e 3 e somar com a do triângulo de 3 a 4:
Passo 4
Para o percurso de 6m:
Vamos pegar a área que já tínhamos até 4m e somar com a do retângulo que aparece entre 4m e 6m:
Passo 5
Para o percurso de 6m:
Vamos pegar a área que já tínhamos até 6m e somar com a do triângulo que aparece entre 6m e 7m:
Passo 6
Agora só falta calcular as velocidades, chega junto! Vamos isolar a velocidade final partindo da fórmula da variação da energia cinética:
Então, vamos só substituir os valores nessa fórmula, para cada caso que queremos!
Passo 7
Para 2m:
Para 3m:
Como , para 4m:
Analogamente, para 6m
E para 7m: