Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 7.Problemas - Ex. 5
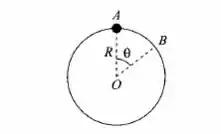
Uma conta de massa m, enfiada num aro circular de raio R que está num plano vertical, desliza sem atrito da posição A, no topo do aro, para a posição B, descrevendo um ângulo (Fig.). a) Qual é o trabalho realizado pela força de reação do aro sobre a conta? b) Qual é a velocidade da conta em B?
Passo 1
- É essencial notar aqui que a força de reação do aro na conta é a força normal que atua nela. Essa foça não contribui para o trabalho realizado na conta já que está sempre perpendicular ao movimento, tranquilo? Por isso
- A normal não realiza trabalho, mas a força gravitacional sim, hehe. Cola mais!
Passo 2
Aqui é só a gente calcular a variação de energia potencial gravitacional de A pra B, tranquilo?
Vamos olhar pra figura
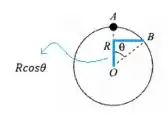
Pronto, daqui sabemos que nossa altura e
Como
Resposta
Exercícios de Livros Relacionados
A FIGURA PD13.76 mostra uma partícula de massa m a uma distância x do centro de um cilindro muito fino, de massa M e comprimento L. A partícula se encontra fora do cilindro, de modo que xL/2. a. Calcu
Imagine que seu trabalho para a NASA seja monitorar órbitas de satélites. Um dia, durante uma pesquisa de rotina, você descobre que um satélite de 400 kg, em órbita circular a 1.000 km de altitude, ir
A FIGURA PD13.77 mostra uma partícula de massa m a uma distância x ao longo do eixo de um anel muito fino de massa M e raio R. a. Calcule a energia potencial gravitacional dessas duas massas. b. Use o
A F i g13 - 43 mostra quatro partículas, todas de massa 20.0g , que formam um quadrado de lado d = 0.600m . Se d é reduzido para 0.200m , qual é a variação da energia potencial gravitacional do sistem
A F i g13 - 43 mostra quatro partículas, todas de massa 20.0g , que formam um quadrado de lado d = 0.600m . Se d é reduzido para 0.200m , qual é a variação da energia potencial gravitacional do sistem