Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 6.Problemas - Ex. 11
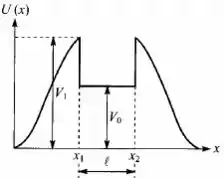
Uma partícula de massa m move-se em uma dimensão com energia potencial U(x) representada pela curva da Fig.( as beiradas abruptas são idealizações de um potencial rapidamente variável. Inicialmente a partícula está dento do “poço de potencial” ( região entre ) com energia E tal que . Mostre que o movimento subsequente será periódico e calcule o período.
Passo 1
A energia mecânica da partícula é dada por
Isolando a velocidade,
Integrando os dois lados em relação ao tempo temos
Para que haja solução para essa equação devemos ter sempre . Como nossa energia mecânica do problema está definida como o corpo sempre irá assumir posições cujo potencial é menor que . Para atingir outras posições fora de em que o potencial é menor que a energia mecânica, seria necessário um trabalho externo a fim de superar a barreira de potencial . Se isso não acontece o corpo oscila entre .
Passo 2
Como a distância a ser percorrida para retornar ao mesmo ponto do sistema é de , nosso período se torna uma vez que a força resultante no corpo é 0 (potencial constante).