Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 7.Problemas - Ex. 19
Um garotinho esquimó desastrado escorrega do alto do seu iglu, um domo esférico de gelo de 3m de atura. a) De que altura acima do solo ele cai? b) A que distância da parede do iglu ele cai?
Passo 1
- Pessoal, vamos primeiro observar um esquema do problema pra entendermos melhor, ok?
- Vamos viajar de volta pros capítulos iniciais e resolver essa parada, mas antes precisamos saber da velocidade na hora em que o garoto perdeu o contato com o iglu. Mas, felizmente a gente já calculou isso!
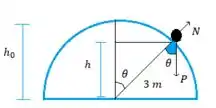
O menino quando está num ponto qualquer da trajetória tem duas forças atuantes em seu corpo, o peso e a normal , vamos lá escrever as equações
Se queremos avaliar o momento em que ele escorrega do iglu, quer dizer que ele perde contato com a superfície do gelo e isso significa que a força normal é igual a 0, fechou?
Como essa força é a resultante centrípeta temos o seguinte
Para a gente saber a altura em que isso acontece vamos ver o trabalho que a força gravitacional exerceu até chegar nessa velocidade.
Putz... e agora? Esse ângulo ai como que é que faz, finge que não existe? Não, hehe. Vamos olhar pro nosso esqueminha lá em cima. Sabemos que pelo triângulo
Passo 2
OK, mas não acabou ainda... a gente vai ter que descobrir pra decompor nossas velocidades.
Olha só como fica nosso esquema pra a velocidade
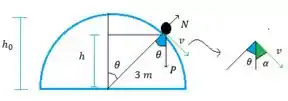
Daqui sabemos que , mas como
Show, temos tudo para montar nossas equações horárias, se liga aqui!
(Usando a eq. Vertical)
(Aplicando o tempo encontrado na eq. Horizontal)
Passo 2
Opa, mas essa é a distância a partir do início da queda e não do iglu! Cuidado aí, rsrs. Pra calcular a distância real precisamos ver qual é a distância do ponto inicial pro final do iglu.
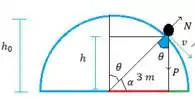
Queremos a distância verde, que é o raio do iglu menos a distância vermelha
Finalmente pra matar a questão a distância do ponto de queda pro iglu é