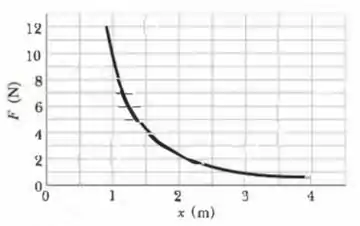
Uma partícula que se move ao longo de um eixo x está submetida a uma força orientada no sentido positivo do eixo. A Fig. 7-48 mostra o módulo F da força em função da posição x da partícula. A curva é dada por F = a / x 2 , com a = - 9,0N ∙ m 2 . Determine o trabalho realizado pela força sobre a partícula quando a partícula se desloca de x = 1,0m para x = 3,0m (a) estimando o trabalho a partir do gráfico e (b) integrando a função da força.

W á r e a = 7,00J á ; W i n t e g r a l = 6,00J .

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.Problemas Adicionais - Ex. 79

Uma partícula que se move ao longo de um eixo está submetida a uma força orientada no sentido positivo do eixo. A Fig. 7-48 mostra o módulo da força em função da posição da partícula. A curva é dada por , com . Determine o trabalho realizado pela força sobre a partícula quando a partícula se desloca de para (a) estimando o trabalho a partir do gráfico e (b) integrando a função da força.

Passo 1

Olá! Tudo bom?

A questão pede para calcular o trabalho sobre a partícula de duas formas diferentes! Mas antes de começar temos que lembrar a definição de trabalho é o produto da força aplicada durante um deslocamento.

Deste modo, uma forma de acharmos o tralbaho através do gráfico é calculando a área sob a superfície no deslocamento dado.

Para estimar o valor do trabalho realizado pela força de até , vamos calcular a área do gráfico da força em função do deslocamento nos intervalos acima. Então, vamos dividir a figura em duas partes:

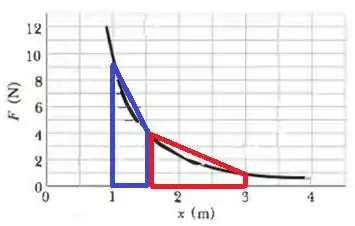
Para calcular essa área teremos que fazer uma aproximação com a figura geométrica mais próxima. Então, vamos calcular a área dos dois trapézios acima. Assim:

Portanto, o trabalho total é:

Passo 2

Para calcular o trabalho por integração, devemos lembrar que:

Montando a integral com os dados do problema:

Repara que os limites de integração são o deslocamento.

Agora podemos integrar!

Repara que houve uma pequena diferença nos cálculos, isso se deve a aproximação realizada pelo calculo da área.

Resposta

;
.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Como você compara o trabalho realizado para esticar uma mola de 2,0 cm, a partir da configuração frouxa, com o trabalho necessário para esticá-la de 1,0 cm, a partir da configuração frouxa?

Mostre que a unidade SI para a constante de força de uma mola pode ser escrita como k g / s 2 .

A dimensão da potência é (a) M * L^2 * T^2 , (b) M * L^2 // T , (c) M * L^2 // T^2 , (d) M * L^2 // T^3 .

Determine a potência desenvolvida por uma força F → que atua sobre uma partícula que se move a velocidade v → , onde (a) F → = 4,0N i ^ + 3,0N k ^ e v → = ( 6,0m / s ) i ^ ; (b) F → = 6,0N i ^ - 5,0N

A força A realiza 5,0 J de trabalho em 10 s. A força B realiza 3,0 J de trabalho em 5,0 s. Qual das duas forças desenvolve maior potência? Explique.