Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.Problemas Adicionais - Ex. 95
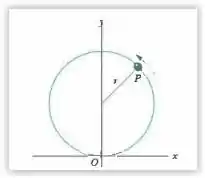
Uma partícula se move com velocidade escalar constante sobre uma circunferência de raio (Fig. 4 56) e completa uma revolução a cada . A partícula passa pelo ponto no instante . Os vetores pedidos a seguir devem ser expressos na notação módulo ângulo (ângulo em relação ao sentido positivo de ). Determine o vetor posição da partícula, em relação a , nos instantes (a) , (b) e (c) . (d) Determine o deslocamento da partícula no intervalo de entre o fim do quinto segundo e o fim do décimo segundo. Para esse mesmo intervalo, determine (e) a velocidade média e a velocidade (f) no início e (g) no fim do intervalo. Finalmente, determine a aceleração (h) no início e (i) no fim do intervalo.
Passo 1
Então pessoal , a primeira coisa que devemos fazer é escrever os vetores na forma módulo-ângulo (). Como de costume os ângulos são medidos no sentido antihorário a partir do semieixo positivo, mas vamos ocasionalmente nos referir a ângulos que são medidos no sentido anti-horário a partir do semieixo negativo.Sabemos que a velocidade da partícula é dada por :
em que e , dessa forma :
De acordo com a Fig. 4-56, a partícula está se movendo no sentido anti-horário.
Passo 2
Sabemos que no instante , a partícula percorreu uma fração :
de uma revolução completa (começando no ponto da figura, ou seja, no semieixo negativo). Assim, o ângulo descrito pela partícula em relação ao semieixo negativo pode ser calculado simplesmente pela relação :
Como se pode ver na figura, as coordenadas desse ponto são e no sistema de coordenadas da figura. Na notação módulo-ângulo, o vetor posição desse ponto é . Embora essa posição seja fácil de analisar sem recorrer a relações trigonométricas , é uma boa notar que esses valores das coordenadas e podem ser obtidos a partir do ângulo usando as relações :
Tranquilo até aqui ?
Naturalmente, os valores do módulo e do ângulo foram obtidos usando as equações e .
Passo 3
De forma análoga ao item anterior , no instante , a partícula percorreu uma fração de revolução. O ângulo descrito pela partícula , por sua vez , é . As coordenadas desse ponto são: e ; o vetor posição do ponto é .
Passo 4
Nós sabemos também que no instante , a partícula percorreu uma fração de revolução. O ângulo descrito pela partícula é . As coordenadas desse ponto são e ; o vetor posição do ponto é .
Passo 5
Subtraímos o vetor posição obtido no item (a) do vetor posição obtido no item (c):
usando a notação módulo-ângulo. Na notação dos vetores unitários, teríamos :
O que levaria ao mesmo resultado, e
Passo 6
Nós sabemos que a velocidade média é dada por .Logo , para , temos:
na notação dos vetores unitários ou na notação módulo-ângulo.
Passo 7
Bom pessoal , o módulo da velocidade da partícula já foi calculado (); para conhecer a direção podemos analisar a figura do enunciado . Como o vetor velocidade é tangente à circunferência na posição de “3 horas” , isso significa que é vertical. Assim, a resposta é ().
Passo 8
Mais uma vez, o módulo da velocidade é conhecido () e a direção pode ser determinada observando . O vetor velocidade é tangente à circunferência na posição de “12 horas” , o que significa que é horizontal. Assim, a resposta é ().
Passo 9
A aceleração tem módulo , e no instante inicial é horizontal (na direção do centro da circunferência). Assim, a resposta é ().
Passo 10
Mais uma vez, temos que :
mas nesse instante a aceleração é vertical (na direção do centro da circunferência). Assim, a resposta é ().
Tranquilo pessoal ?? Bora resolver mais questões então!!!!
Resposta
Ei, a resposta está no passo a passo :)