Você leva a filha pequena de seu vizinho a um parque de diversões para brincar em diversos brinquedos. Ela quer ir no brinquedo chamado O Foguete. Oito assentos em forma de foguetes são suspensos por correntes à borda de um grande disco de aço. Um eixo vertical passa pelo centro do disco e o faz girar; assim, os foguetes de brinquedo passam a descrever círculos horizontais. Você acaba de ter aula de física, de modo que decide descobrir o valor da velocidade dos foguetes enquanto espera. Você, então, estima que o disco tenha uns de diâmetro, e as correntes, de comprimento. O brinquedo leva para atingir a velocidade final, quando as correntes formam com a vertical. Quanto vale a velocidade do foguete?
Passo 1
Olá, tudo bem?
Vamos anotar todos os dados que o problema nos dá:
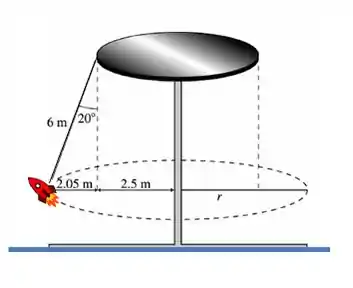
Agora dá uma olhada nesse desenho que fiz da situação:
Pelo desenho, a gente consegue ver que o raio da trajetória não é igual ao raio do disco de aço no qual as cordas estão presas. Quando o disco começa a girar, as cordas fazem um ângulo de com a vertical, aumentando o raio da trajetória. Esse aumento vai estar relacionado com o cosseno do ângulo de abertura e o comprimento da corda:
E assim o raio da trajetória é:
Passo 2
Vamos agora considerar o foguete uma partícula e fazer um diagrama de corpo livre para ele. Temos basicamente duas forças: a força da gravidade , apontando verticalmente para baixo e a força tensora , que aponta para cima ao longo da corda e faz um ângulo de com a vertical. O desenho fica assim ó:
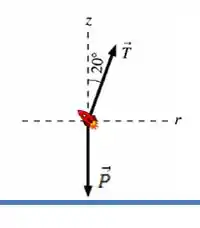
Sendo assim, temos um sistema:
Vamos agora dividir a primeira equação pela segunda. Com isso vamos ter uma relação para a velocidade , as massas e as tensões vão ser canceladas:
Usando que é igual a , podemos simplificar essa expressão:
Passo 3
Tranquilo até aqui?
Agora vamos resgatar o valor de do passo e substituir na expressão que acabamos de determinar pra velocidade:
E essa é a velocidade do foguete!
Beleza?
Espero ter ajudado!
Vamos pra próxima?