Uma partícula move-se ao longo da direção x sob o efeito de uma força , onde . a) Calcule a energia potencial U(x) da partícula, tomando U(0) = 0, e faça um gráfico de U(x) para -0,5m
Dado :
Passo 1
- Bom galera, como sabemos que
- As posições de equilíbrio são as posições em que a força resultante se torna 0, então vamos substituir na nossa fórmula de força e descobrir quais são os pontos do eixo x.
- No gráfico de U(x) se uma partícula está em ela irá descrescer seu potencial indefinidamente, adquirindo mais e mais enrgia cinética. Para que um movimento oscilatório ocorra, a energia cinética e potencial precisam estar se revesando a cada ciclo, ou seja, a partícula estaria “subindo e descendo” no gráfico de potencial. Isso acontece se a partícula for perturbada para a esquerda quando estiver em .
- Após a partícula acelera e antes de a partícula desacelera.
Vamos calcular
Mas o problema diz que . Então nossa função se torna
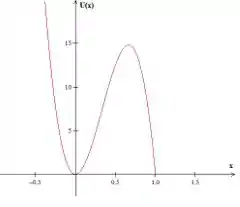
Nosso gráfico fica assim
Passo 2
No gráfico de potencial, para sair do ponto 0 existe uma barreira de potencial de ambos os lados, de modo que se a partícula se mover pra qualquer um deles sua tendência é voltar para o local de menor energia. Por isso 0 é um ponto de estabilidade. Já o ponto representa um pico nesse gráfico, se a partícula for perturbada facilmente sai dessa posição para locais de menor energia potencial. Então é um ponto de instabilidade
Passo 3
Nesse momento sua energia cinética é 0 e sua energia mecâncica total . Como queremos descobrir o ponto de retorno, sua velocidade terá que ser 0 novamente. Vamos buscar por
Outro ponto que satisfaz esse valor à esquerda do gráfico é
Então nossa região de movimento oscilatório corresponde a
Já a energia mecância