Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 2.Exercícios e Problemas - Ex. 7

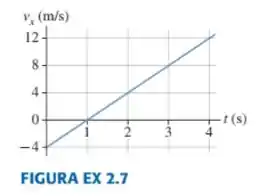
Uma partícula parte de x 0 =   10   m em t 0 = 0   s e move-se de acordo com o gráfico da velocidade da FIGURA EX 2.7.

  1. A partícula tem um ponto de retorno? Em caso afirmativo, em que instante?
  2. Qual é sua posição em t = 2   s , t = 3   s e t = 4   s ?

Passo 1

  1. A partícula tem um ponto de retorno? Em caso afirmativo, em que instante?

    2. Tem que ficar atento ao tipo de gráfico que temos. A questão nos fornece um gráfico de velocidade versus tempo.

    Dizemos que temos um ponto de retorno quando a velocidade muda de sinal, porque isso significa que a partícula estava andando em um sentido e passa a andar no outro sentido.

    Analisando o gráfico, vemos que a partícula começa com uma velocidade negativa, v =   - 4   m / s e essa velocidade vai aumentando até que em t = 1   s ela atinge velocidade zero e passa a ter uma velocidade positiva.

    Notou que em t = 1   s   a velocidade mudou de sinal? Então é aí que temos o nosso ponto de retorno, Show né?

    Passo 2

  2. Qual é sua posição em t = 2   s , t = 3   s e t = 4   s ?

Para resolver essa questão, precisamos de lembrar que:

A ÁREA DO GRÁFICO VELOCIDADE VERSUS TEMPO NOS FORNECE A DISTÂNCIA PERCORRIDA PELA PARTÍCULA

Isso é importante ein, guarda no coração!!

Então para calcular a posição da partícula em determinado instante devemos seguir essa fórmula:

x f = x 0 + d i s t â n c i a   p e r c o r r i d a

x f = x 0 + á r e a   d o   g r á f i c o   e n t r e   t 0   e   t f

Beleza?

Passo 2

A posição inicial é dita na questão

x 0 = 10   m

Para t = 2   s

x 2 s = 10 - á r e a   d o   t r i â n g u l o   e n t r e   0 s   e   1 s + ( á r e a   d o   t r i g â n g u l o   e n t r e   1 s   e   2 s )

A área do triângulo entre 0 s e 1 s é subtraída porque está abaixo do eixo x do gráfico, okay? As áreas que estão acima do eixo x são somadas.

x 2 s = 10 - 1 2 . 1 .   4 + 1 2   .   1 .   4 = 10 - 2 + 2 =   10   m  

Para t = 3   s

x 3 s = 10 - á r e a   d o   t r i â n g u l o   e n t r e   0 s   e   1 s + ( á r e a   d o   t r i g â n g u l o   e n t r e   1 s   e   3 s )

x 3 s = 10 - 2 + 1 2   .   2 .   8 = 10 - 2 + 8 =   16   m  

Para t = 4 s

x 4 s = 10 - á r e a   d o   t r i â n g u l o   e n t r e   0 s   e   1 s + ( á r e a   d o   t r i g â n g u l o   e n t r e   1 s   e   4 s )

x 4 s = 10 - 2 + 1 2   .   3 .   12 = 10 - 2 + 18 =   26   m

Resposta

  1. Há um ponto de retorno, em t = 1 s

x 2 s = 10   m

x 3 s = 16   m

x 4 s = 26   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um videogame, um ponto é programado para se deslocar na tela de acordo com a função x = 9,00 t - 0,750 t 3 , onde x é a distância em centímetros em relação à extremidade esquerda da tela e t é o te
A Figura 2.42 mostra o gráfico de dados coletados de uma pulga saltitante de 210 μ g em umfilme de alta velocidade ( 3500q u a d r o s / s e g u n d o ). Essa pulga tinha aproximadamente 2m m de compr
A aceleração de um ônibus é dada por a x t = α t , onde α = 1,2m / s 3 . a) Se a velocidade do ônibus para t = 1 , 0 s é igual a 5,0m / s , qual é sua velocidade para t = 2,0s ? b) Se a posiçãodo ônib
O gráfico na Figura 2.43 descreve a aceleração em função do tempo para uma pedra que rola colina abaixo, a partir de uma posição de repouso. a) Determine a variação na velocidade da pedra, entre t = 2