Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.6 - Ex. 50

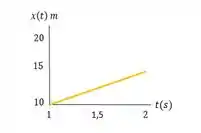
A aceleração de um ônibus é dada por a x t = α t , onde α = 1,2   m / s 3 . a) Se a velocidade do ônibus para t = 1 , 0 s é igual a 5,0   m / s , qual é sua velocidade para t = 2,0   s ? b) Se a posição

do ônibus para t = 1,0   s é igual a 6,0   m , qual sua posição para t = 2,0   s ? c) Faça gráficos a t , v t   e x t para esse movimento.

Passo 1

Show de bolinhas pessoal! Nessa questão temos um ônibus acelerado e quando o movimento é acelerado, temos que:

v = v 0 + a ⋅ t

E além disso, temos a equação horaria, dada como:

S = S 0 + v 0 t + a t 2 2

Mas, aqui, a aceleração não é constante (o enunciado nos informa que ela é dada por a x t = α t ). Então não podemos utilizar as equações de aceleração constantes. Em vez disso, vamos usar:

v = v 0 + ∫ 0 t a ⋅ d t

Nessa equação, podemos achar a velocidade, v em qualquer tempo;

E, na próxima equação, podemos encontrar a posição, S , em qualquer tempo:

S = S 0 + ∫ 0 t v ⋅ d t

Bora lá!

Passo 2

  1. Vamos começar então montando a nossa integral, substituindo a a acelaração fornecida:

    2. v = v 0 + ∫ 0 t α t   d t

    Iradoso, agora vamos relembrar como calculamos integral com exponencial:

    ∫ t n d t = t n + 1 n + 1

    Resolvendo a integral ficamos com

    v = v 0 + α t 2 2

    Agora vamos aplicar!

    Passo 3

    Para responder a letra a temos as seguintes informações:

    Dados : α = 1,2   m / s 3 t = 1 , 0   s v = 5,0   m / s

    Aplicando em,

    v = v 0 + α t 2 2

    Portanto, obtemos que:

    5   m/s = v 0 + 1,2   m/ s 3 ) ( 1   s 2 2

    v 0 = 4,4   m/s

    Encontramos a velocidade inicial, v 0 , então, quando t = 2   s , encontramos sua velocidade nesse intervalo de tempo:

    v = 4,4   m/s + ( 0,60   m/ s 3 ) 2   s 2    

    v = 6,8   m/s

    Passo 4

  2. A letra b vamos fazer de forma análoga!

Agora, vamos montar a integral da posição com os dados que temos:

Dados : S = 6   m t = 1   s α = 1,2   m / s 3

S = S 0 + ∫ 0 t v ⋅ d t

Como v = v 0 + α t 2 2 , então vamos obter que:

  S = S 0 + ∫ 0 t ( v 0 + a t 2 2 )  

S = S 0 + v 0 t + α t 3 6

Logo:

6   m = S 0 ⋅ 1 + 1,2   m/ s 3 ⋅ 1   s 3 6

S 0 = 1,4   m

Encontramos a posição inicial, S 0 , então, quando t = 2 s , encontramos sua velocidade nesse intervalo de tempo, tal que:

S = 1,4   m + 4,4   m/s ⋅ 2   s + 1,20   m/ s 3 ⋅ 2   s 3 6

S = 11,8   m

Passo 3

E por fim, temos que:

x t = 1,4   m + 4,4   m/s ⋅ t + 0,20   m/ s 3 ⋅ t 3

v t = 4,4   m/s + 0,60   m/ s 3 ⋅ t 2

a t = 1,20   m/ s 3 ⋅ t

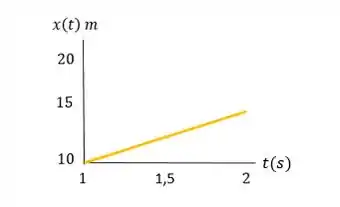
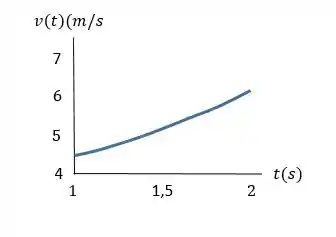
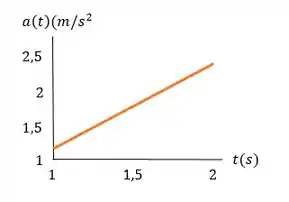
Resposta

v 0 = 4,4   m/s   e v = 6,8   m/s

S 0 = 1,4   m   e S = 11,8   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A FIGURA P2.28 Mostra o gráfico da aceleração de uma partícula que parte do repouso em t =0s . Determine sua velocidade nos instantes t =0s ,2s ,4s ,6s ,e8s .
Um trem com uma velocidade constante de 60,0k m / h se move na direção leste por 40,0m i n , depois em uma direção que faz um ângulo de 50,0 º º a leste com a direção norte por 20,0m i n e, finalmente
A posição de um corpo varia segundo a equação x = Ac o s ⁡ ( ω t ) . Calcule a velocidade e aceleração do corpo no instante t .
A posição de um corpo varia segundo a equação x = As e n ⁡ ( ω t ) . Mosre que x = - a / ω 2 , onde a é a aceleração do corpo.
A velocidade de um corpo varia segundo a equação: v = 6m s + 0,2 m s 3 ⋅ t 4 Qual a aceleração do corpo no instante t = 2s ? Qual é o seu deslocamento no intervalo entre t = 2s e t = 4s ?