Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 8.Problemas - Ex. 90

Suponha que você mantenha uma bola pequena em contato com uma bola grande diretamente sobre seu centro. Se você largar a bola pequena um pequeno intervalo de tempo após largar a bola grande, a bola pequena será rebatida para cima com uma velocidade surpreendente. Para exemplificar o caso extremo, despreze a resistência do ar e suponha que a bola grande faça uma colisão elástica com o solo, a seguir suba e colida elasticamente com a bola pequena que ainda está descendo. Imediatamente antes da colisão entre as duas bolas, a bola grande sobe com velocidade v → , e a bola pequena está descendo com velocidade v → . (Você sabe por quê?) Suponha que a bola grande possua massa muito maior do que a da bola pequena. a) Qual é a velocidade da bola pequena imediatamente depois da colisão com a bola grande? b) Usando a resposta do item (a), ache a razão entre a distância percorrida pela bola pequena quando ela retorna para cima e a distância que ela percorreu antes da colisão.

Passo 1

v 1 é positiva e v 2 é negativa.

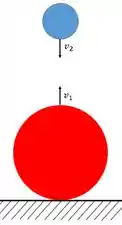
Por se tratar de uma colisão perfeitamente elástica, temos que

v 2 f = v 1 f - v 2 i + v 1 i

Supondo que a massa da bola maior seja muito maior que a menor, temos que pela conservação de momento, a velocidade da bola grande não deve se alterar significativamente. Sendo assim temos que

v 1 f ≈ v 1 i

Passo 2

  1. Usando a relação

    2. v 2 f = v 1 f - v 2 i + v 1 i =   v - - v + v = 3 v

    Sendo assim temos que a bola pequena sobe com uma velocidade 3 v .

    Passo 3

  2. Vamos usar o princípio da conservação de energia, onde imaginando a bola grande caindo, partindo do repouso, temos que K i = 0 . Quando a bola atinge o chão, temos que U f = 0 . Sendo assim temos

U i = K f

m g h = m 2 v 2

Logo a altura que ambas as bolsas foram soltas foi

h = v 2 2 g

Porém pensando apenas na bola grande, temos que quando ela toca o chão e sofre uma colisão perfeitamente elástica, ela volta a subir a mesma altura h 1 .

Em compensação, a bola menor deve subir uma altura maior.

Pelo princípio da conservação de energia temos

m g h 2 = m 2 3 v 2 → h 2 = 9 v 2 2 g = 9 h 1

Resposta

  1. 3 v
  2. h 1 = v 2 2 g e h 2 = 9 h 1
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

44 . Um bloco de 15,0k g é preso a uma mola horizontal muito leve com constante de força 500,0N / m e está apoiado sobre uma mesa horizontal sem atrito (Figura E8.44). De repente, o bloco é atingido p
39 . João (massa 55,0k g ) está deslizando rumo leste com velocidade de 8,00m / s sobre a superfície de um lago congelado. Ele colide com Jonas (massa 48,0k g ), que está inicialmente em repouso. Após
74 . O bloco B (massa de 4,00k g ) está em repouso na borda de uma plataforma lisa, a 2,60m acima do piso. O bloco A (massa de 2,00k g ) desliza com uma velocidade de 8,00m / s ao longo da plataforma
70 . Você e seus amigos estão fazendo uma experiência de física sobre um lago congelado que serve como uma superfície horizontal, sem atrito. Samuel, com massa de 80,0k g , é empurrado e desliza na di
75 . Dois blocos têm uma mola comprimida entre eles, como no Exercício 8.24. A mola tem força constante de 720N / m e, inicialmente, é comprimida0,225m de seu comprimento original. Para cada bloco, qu