Em uma partida de beisebol, o monte do arremessador fica 0,20 m acima do nível do campo e a 18,4 m da base. Um arremessador atira uma bola com uma rapidez inicial de 37,5 m/s. No momento em que a bola abandona a mão do arremessador, ela está 2,30 m acima do monte. (a) Qual deve ser o ângulo entre e a horizontal para que a bola cruze a base 0,70 m acima do chão? (Ignore a resistência do ar.) (b) Com que rapidez a bola cruza a base?

Oi pessoal, tudo bem? Nesse tipo de problema, a primeira coisa a se fazer é tentar visualizar a situação. Pra te ajudar trouxe aqui um desenho que esquematiza tudo certinho.

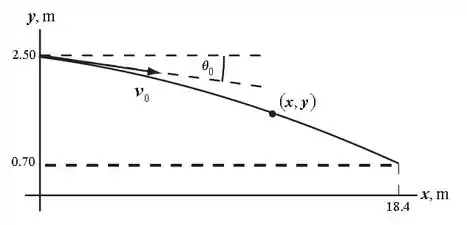
Analisando o desenho é possível observar que o movimento se inicia a uma altura de 2,50 m do chão. Isso porque a questão nos diz que a bola sai da mão do arremessador a 2,30 m do monte e o monte tem 0,2 m. E o que a questão te pede é qual o ângulo entre e a horizontal para que a bola cruze a base (que está a 18,4 m do arremessador) a uma altura de 0,70 m do chão. Conseguiu visualizar? Então vamos partir pras continhas.

Nossa velocidade pode ser decomposta em uma velocidade e caracterizando um movimento na horizontal e outro na vertical. O movimento da horizontal (em x) não possui aceleração, ou seja, ela é zero. Então o movimento é uniforme. Por isso para resolver o problema usaremos:

Onde

Na vertical, como a aceleração é a gravidade, o movimento é acelerado. Por isso podemos usar as equações:

Onde

Como na questão não nos foi dado o tempo do movimento, podemos fazer manipulações com as equações, já que o tempo em x é o mesmo em y.

Substituindo as componentes e temos:

Agora podemos substituir os valores dados na questão:

Resolvendo na calculadora temos que .