Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 108

Um jogador de futebol americano faz um lançamento (manual) a um ângulo de 36,5° acima da horizontal, em um ponto distante 3,50 m do ponto de onde partiu, 2,50 s antes, aquele que deve receber o passe. A rapidez deste companheiro é constante, de 7,50 m/s Para que a bola chegue às mãos do companheiro, com que rapidez o lançamento deve ser feito? Suponha a bola lançada e recebida à mesma altura. (Ignore a resistência do ar.)

Passo 1

E aí galera, beleza? Bom... Se você não entende nada de futebol americano não precisa se desesperar porque esse problema é física pura. Primeiro tenta sempre visualizar a situação acontecendo. Mas se não conseguiu visualizar, analisa a figura abaixo.

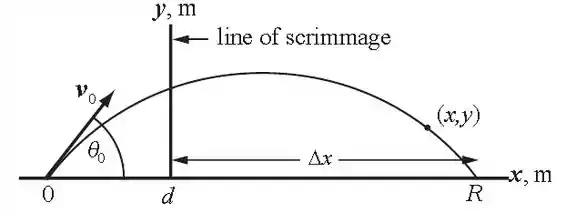
O problema envolve o lançador e o receptor. O receptor inicialmente está a 3,5 m do lançador, na linha de scrimmage como apresentado na imagem. O receptor começa a correr a uma velocidade constante de 7,5 m/s e depois de 2,5 s a bola é lançada. O problema quer saber a velocidade de lançamento para que o receptor possa pegar a bola.

Podemos notar que o tempo de vôo da bola e de corrida após os 2,5 s deve ser o mesmo para que o receptor consiga interceptar a bola.

Primeiro vamos dividir o problema em movimento do receptor e movimento da bola e aí vamos relacionar os dois movimentos.

Primeiro vamos ao movimento do receptor:

Ele está em movimento com velocidade constante, portanto as equações de movimento uniforme regem seu movimento. Vamos usar as nomenclaturas do desenho para facilitar.

∆ x = v ⋅ ∆ t t o t a l

Onde ∆ t t o t a l = ∆ t b o l a + 2,5 .

Passo 2

O movimento da bola é regido pelas equações do movimento oblíquo que é a junção de um movimento uniforme e um movimento uniformemente variado.

Temos que:

∆ x b o l a = v 0 x ⋅ ∆ t b o l a

Onde ∆ x b o l a = ∆ x + 3,5 .

v ⋅ ( ∆ t b o l a + 2,5 ) + 3,5 = v 0 ⋅ cos ⁡ 36,5 ° ⋅ ∆ t b o l a

Passo 3

Agora vamos relacionar as equações:

∆ x b o l a = v 0 x ⋅ ∆ t b o l a

Mas:

∆ x b o l a = ∆ x + 3,5

Então:

∆ x + 3,5 = v 0 x ⋅ ∆ t b o l a

Temos também que:

∆ x = v ⋅ ∆ t t o t a l

Então:

v ⋅ ∆ t t o t a l + 3,5 = v 0 x ⋅ ∆ t b o l a

Podemos dizer ainda que:

∆ t t o t a l = ∆ t b o l a + 2,5

Então chegamos a seguinte equação:

v ⋅ ( ∆ t b o l a + 2,5 ) + 3,5 = v 0 ⋅ cos ⁡ 36,5 ° ⋅ ∆ t b o l a

Para acharmos a velocidade inicial v 0 precisamos saber o tempo de voo da bola.

Otempo de voo é dado por:

y = y 0 + v 0 y ⋅ t - 1 2 g t 2

0 = 0 + v 0 ⋅ sin ⁡ 36,5 ° ⋅ ∆ t b o l a - 1 2 ⋅ 9,81 ⋅ ∆ t b o l a 2

v 0 ⋅ sin ⁡ 36,5 ° = 1 2 ⋅ 9,81 ⋅ ∆ t b o l a

∆ t b o l a = v 0 ⋅ sin ⁡ 36,5 ° ⋅ 2 9,81

∆ t b o l a = v 0 ⋅ 0,1213

Agora podemos substituir para termos somente termos em função de v 0 na equação:

v ⋅ ( v 0 ⋅ 0,1213 + 2,5 ) + 3,5 = v 0 ⋅ cos ⁡ 36,5 ° ⋅ v 0 ⋅ 0,1213

Temos:

0,0975 v 0 2 - 0,91 v 0 - 22,25 = 0

Resolvendo, podemos encontrar o valor:

v 0 = 20,5   m / s

Resposta

v 0 = 20,5   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um projétil é disparado com uma velocidade inicial v 0 = 30,0m / s , a partir do solo, com o objetivo de atingir um alvo que está no solo a uma distância R = 20,0m , como mostra a figura. Quais são (a
129- Em uma partida de softball, o lançador arremessa a bola de um ponto situado 3,0 pés acima do solo. Um gráfico estroboscópico da posição da bola é mostrado na Fig. 4-60, em que as leituras estão s
138- Uma mulher é capaz de fazer um barco a remo atingir uma velocidade de 6,40 km/h em água parada. (a) Se a mulher está atravessando um rio no qual a correnteza tem uma velocidade de 3,20 km/h, em q
124- Uma surpresa gráfica. No instante t = 0 , uma bola é lançada a partir do solo plano, com uma velocidade inicial de 16,0 m/s e um ângulo de lançamento θ 0 . Imagine um vetor posição que ligue o po
61 . A aceleração inicial de um esquiador profissional sobre neve fresca corresponde a 90 % da que seria esperada sobre um plano inclinado sem atrito, sendo a perda devido ao atrito. Devido à resistên