Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 73
Partindo do repouso, uma força constante é aplicada à extremidade livre de um cabo de enrolado em volta da borda externa de um cilindro maciço e uniforme, semelhante ao da situação indicada na Figura 10.9a. O cilindro possui massa de e diâmetro de e está livre para girar em torno de um eixo fixo e livre de atrito que passa pelo seu centro.
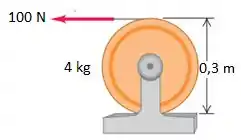
a) Quanto tempo leva para que todo o cabo se desenrole e com que velocidade o cabo está se movendo quando a última parte se liberta?
b) Agora, suponha que o cilindro seja substituído por um aro uniforme, mas que todas as demais grandezas permaneçam inalteradas. Nesse caso, as respostas ao item (a) seriam maiores ou menores? Explique.
Passo 1
Eaee, belezinha??? Bom... o enunciado nos diz que uma força constante , que parte do repouso, é aplicada à extremidade livre de um cabo de enrolado em volta da borda externa de um cilindro maciço e uniforme, como mostra abaixo a figura:
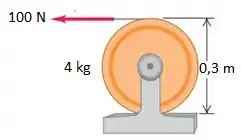
Queremos calcular o tempo que leva para que todo o cabo se desenrole e com que velocidade o cabo está se movendo quando a última parte se liberta.
Em seguida, devemos fazer a mesma coisa, mas supondo agora que o cilindro seja substituído por um aro uniforme, mas que todas as demais grandezas permaneçam inalteradas.
Para isso, temos que saber que:
Onde é o torque, é a aceleração angular e é o momento de inércia.
Passo 2
- Então nessa questão você tem que se ligar que essa força puxa o fio e com isso ele vai desenrolando. Então vamos relembrar as fórmulas para o torque, a primeira é dada como:
Ou seja, o produto entre o momento de inércia e a aceleração angular .
A outra fórmula para o torque é dada por:
Isto é, o produto vetorial do raio perpendicular pela força aplicada . Sabendo disso, podemos igualar as duas expressões, de forma que;
Sendo , e o momento de inércia do cilindro dado por , teremos que:
Repara que os se anulam, então:
Passo 3
Agora podemos encontrar a aceleração linear do cilindro e da corda, tal que:
Substituindo os valores que obtemos, vamos descobrir que:
Passo 4
E agora pra descobrir o tempo gasto, podemos usar a equação horaria, dada como:
Como , então...
Logo:
Então, para a velocidade teremos,
De forma que:
Passo 5
Vamos supor que o momento de inércia seja o momento de inércia de um aro uniforme, ou seja,
Como o momento de inércia é maior do que o anterior, a aceleração no aro será menor.
Se essa aceleração é menor, o aro se soltará do cabo com uma velocidade menor que a anterior e levará um tempo maior pra realizar esse movimento.
Vamos ver se é isso mesmo?
A equação do torque ficaria
Passo 6
Comparando com o passo 2, vemos que a aceleração reduziu a metade, ou seja,
No passo 3, escrevemos que
Logo:
E a velocidade seria:
Resposta
a) e .
b) O tempo agora seria e