Uma partícula viaja por um caminho circular, e o ponto está no centro desse círculo. (a) Se o momento linear da partícula é dobrado, sem mudar o raio do círculo, como a magnitude do momento angular em relação ao é afetada? (b) Se o raio do círculo é dobrado, mas a rapidez da partícula é mantida, como muda a magnitude do momento angular em relação ao ponto ?

Vamos começar escrevendo uma expressão para a magnitude do momento angular da partícula em relação ao ponto . Para isso precisamos de um diagrama da situação:

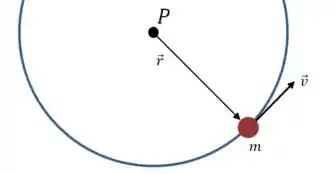
O momento angular da partícula é:

E o módulo de é:

Onde é o ângulo formado pelos vetores e , que nesse caso é :