Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.3 - Ex. 21
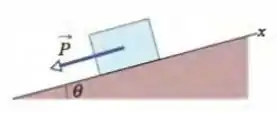
Na Fig. 6-24, uma força atua sobre um bloco com de peso. O bloco está inicialmente em repouso sobre um plano inclinado de ângulo com a horizontal. O sentido positivo do eixo é para cima ao longo do plano. Os coeficientes de atrito entre o bloco e o plano são e . Em termos dos vetores unitários, qual é a força de atrito exercida pelo plano sobre o bloco quando é igual a (a) , (b) e (c) ?
Passo 1
Inicialmente vamos fazer o DCL para facilitar a visualização do problema:
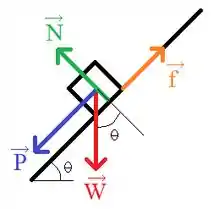
Vamos escrever a segunda lei de Newton para cada eixo:
Passo 2
Vamos calcular o módulo da normal usando a , lembrando que não há movimento no eixo e, portanto, . Assim:
Substituindo os valores e isolando :
Passo 3
Vamos determinar o módulo da força de atrito cinético usando a seguinte relação:
Substituindo os valores conhecidos:
Agora, faremos de maneira análoga para determinar a força de atrito estático máximo, somente trocando da o por :
Substituindo os valores conhecidos:
Passo 4
Nesta etapa, precisaremos ficar bastante atentos, vamos começar a dar valor para a força na e, a partir delas, iremos definir a força de atrito . Para tanto, podemos nos deparar com três casos:
- , então e ;
- , então e calculado nos passos anteriores;
- , então e também calculado nos passos anteriores.
Sem mais delongas, vamos começar a substituir os valores de !
Passo 5
Como , então, caímos no primeiro caso citado e .
Passo 6
Como , então, caímos novamente no prmeiro caso citado e .
Passo 7
Como , então, caímos no terceiro caso citado e .
Passo 8
Como osvalores da força de atrito já foram calculados para cada valor da força dado, precisamos agora escrevê-los em termos dos vetores unitários. Para tanto, precisamos percer que a tendência de movimento ou o movimento sempre é para baixo do plano inclinado e a força de atrito sempre é contrária a isso. Portanto, em todos os casos aqui, a força de atrito tem sentido positivo do eixo , assim:
Resposta
- ;
- ;
- .