Um pássaro voando em um plano possui coordenadas e onde e . a) Faça um esboço da trajetória do pássaro entre e . b) Ache o vetor velocidade e o vetor aceleração do pássaro em função do tempo. c) Ache o módulo, a direção e o sentido do vetor velocidade e do vetor aceleração do pássaro para . d) Faça um esboço do vetor velocidade e do vetor aceleração do pássaro para . Nesse instante, a velocidade escalar do pássaro está aumentando, diminuindo ou é constante? O pássaro está fazendo uma volta? Em caso positivo, em que sentido?
Passo 1
Olá, meu amigo. Yuri aqui e eu estarei te ajudando a resolver.
Temos aqui um pássaro voando e temos sua equação do movimento, tanto para o movimento em quanto para o movimento em . Para encontrarmos a velocidade e a aceleração deveremos derivar a equação do espaço.
Passo 2
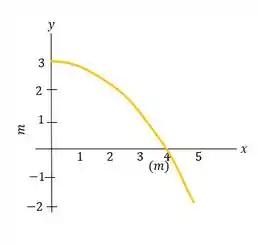
- Primeiro, vamos calcular e para os valores de a :
-
Para encontrarmos a velocidade, derivamos e em função do tempo, :
E
Passo 3
E para encontrarmos a aceleração, derivamos a velocidade:
E
Assim:
E
Passo 4
- Pois então, vamos encontrar a velocidade , quando :
- A aceleração, , tem um componente na mesma direção que , sabemos que está aumentando (o pássaro está acelerando). também possui um componente perpendicular a , de modo que a direção de está mudando; o pássaro está se voltando para para a direita na direção de . é sempre tangente ao caminho; em calculado no item (c) é tangente ao caminho neste , em conformidade com este regra geral. é constante e na direção ; a direção de está virando na direção .
Para :
Temos que e . Dessa forma:
Para :
Temos que: e . Dessa forma:
Com esses valores, construímos o gráfico que é a trajetória do passaro:
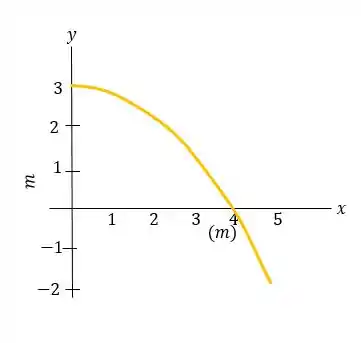
Nós encontramos:
Vamos esboçar a situação:
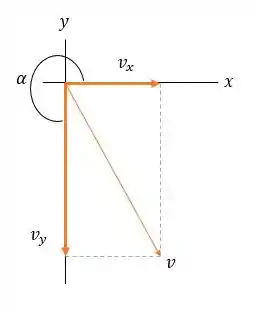
Para encontrarmos , fazemos
Seguindo para encontrar o ângulo , fazemos:
Observando o nosso esboço, temos que:
Passo 4
Agora, vamos encontrar a aceleração, , quando :
Nós encontramos:
Vamos esboçar a situação:
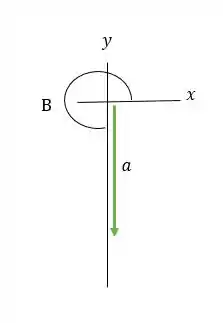
E para encontrarmos , fazemos
Seguindo para encontrar o ângulo , fazemos:
Passo 5
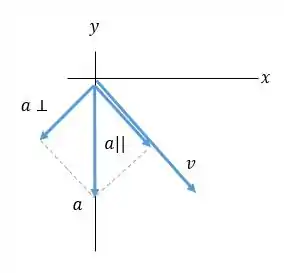
Resposta
-
- e
- e