Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.3 - Ex. 18
A velocidade de um carro em função do tempo é dada por onde e . a) Calcule a aceleração média do carro para o intervalo de tempo de a . b) Calcule a aceleração instantânea para i) ; ii) . c) Desenhe gráficos acurados e para o movimento do carro entre e .
Passo 1
Opa, bora resolver esse problema! O enunciado nos dá uma fórmula da velocidade de um carro em função do tempo:
Onde:
A primeira coisa que devemos responder é a aceleração média do carro para o intervalo de tempo de a .
Sabemos que a aceleração média é dada por:
Nós precisamos usar para encontrar para encontrar para cada .
Então:
Temos também que:
Dessa forma:
Passo 2
Então, aqui, nós precisamos calcular a derivada da função dada para encontrar a aceleração instântanea, .
E para que possamos encontrar a aceleração, , nós precisamos derivar a função .
Vamos relembrar como derivamos função de potencia:
Passo 3
Ok! Então, derivando, encontramos a velocidade instantânea:
Lembrando que a derivada de uma constante é nula! Assim:
Passo 4
Então, quando: :
E quando :
Passo 5
O gráfico da aceleração é uma reta
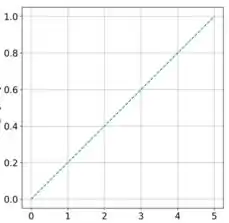
E o gráfico da velocidade é uma parábola:
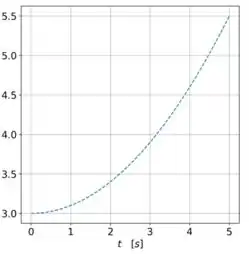
Resposta
a)
b)
c) Gráficos do passo 5