Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 44
Sam, com de massa, deslizando sobre esquis desce uma rampa sem atrito com de altura e de inclinação. Um forte vento de frente exerce sobre ele e os esquis uma força horizontal de . Determine a velocidade de Sam na base da rampa
(a) usando trabalho e energia e
(b) usando as leis de Newton.
Passo 1
A forma de se resolver não é diferente do que fizemos na questão passada , fazendo o esquema dela nós temos:
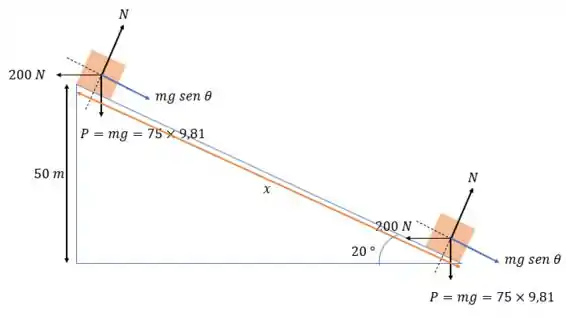
E para resolver esse exercício usando trabalho e energia nós devemos aplicar:
Onde é o trabalho de todas as forças na Sam que é a caixa laranja do desenho (chamei de quadradona ialá). Então a fórmula fica:
Onde é o trabalho causado pela normal, o trabalho da força peso e o trabalho da força do vento (a força de ). E como o trabalho atua na direção do deslocamento, então:
Pois a normal está na perpendicular ao plano.
Onde pelo triângulo retângulo vemos que , então substituindo o que conhecemos:
E o trabalho da força do vento (que é contra o movimento) será:
E considerando a velocidade inicial como nula nós temos:
Passo 2
Agora aplicando as Leis de Newton nós temos que encontrar a força resultante entre a força do peso projetado no plano a força do vento ou seja:
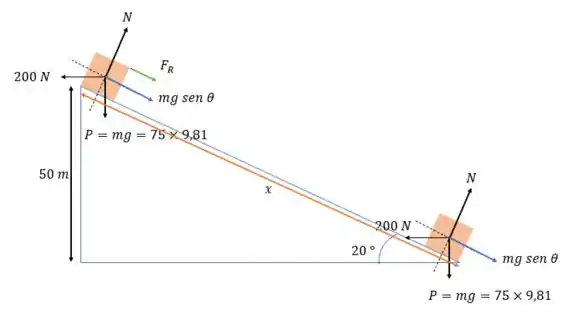
O que nos dá uma aceleração no corpo igual a:
Então por Torricelli a velocidade final da Sam será (para velocidade inicial nula):
Onde
Qualquer mínimo erro é erro de aproximação mesmo.