Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 75
Uma pedra de é rodada por um círculo horizontal na ponta de uma corda longa de . A pedra leva para fazer cada revolução completa. Determine o ângulo que a corda faz com a horizontal.
Passo 1
Vamos desenhar um esquema simples das forças que agem sobre a pedra:
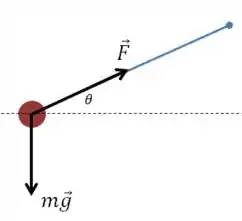
A ideia é que a pedra gire apenas em um plano horizontal, por isso queremos que haja equilíbrio na vertical.
Falta encontrar a força .
Passo 2
A componente horizontal de é a força centrípeta que mantém a trajetória circular da pedra, então:
E podemos calcular a velocidade a partir do período :
Mas o raio da trajetória circular da pedra não é igual ao comprimento da corda:
Então:
Passo 3
Agora é só substituir na fórmula que encontramos lá em cima:
Resposta
A corda faz um ângulo de .
Exercícios de Livros Relacionados
Qual é a velocidade terminal de uma bola esférica de 6,00k g que possui um raio de 3,00c m e um coeficiente de arrasto de 1,60 ? A massa específica do ar no local onde a bola está caindo é 1,20k g / m
Calcule o módulo da força de arrasto a que está sujeito um míssil de 53c m de diâmetro voando a 250m / s em baixa altitude. Suponha que a massa específica do ar é 1,2k g / m 3 e o coeficiente de arras
Uma pequena partícula de poluição se aproxima da Terra, flutuando em ar parado. A rapidez terminal da partícula é 0,30m m / s , a massa da partícula é 1,0.10 - 10g e a força de arrasto da partícula é
Uma demonstração típica de sala de aula envolve soltar filtros de café em forma de cesta e medir o tempo que levam para cair por certa distância. Um professor solta um único filtro de café em forme de
Uma bola de ping-pong tem uma massa de 2,3g e uma rapidez terminal de 9,0m / s . A força de arraste é da forma b v 2 . Qual é o valor de b ?