Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 79
Um piloto de avião de sai de um mergulho através de um arco de círculo cujo raio é , seguindo uma rapidez constante de . (a) No ponto mais baixo do círculo, qual é a direção e a magnitude da aceleração? (b) Qual é a força resultante agindo sobre ele no ponto mais baixo do círculo? (c) Qual é a força exercida no piloto pelo assento do avião?
Passo 1
(a) Podemos representar o movimento do avião por um diagrama como esse:
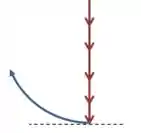
A aceleração centrípeta sempre aponta para o centro da trajetória, então no ponto mais baixo do círculo ela estaria apontando na vertical para cima.
Para calcular sua magnitude, podemos usar a própria definição da aceleração centrípeta:
E já temos a rapidez constante :
Passo 2
(b) E para calcular a força resultante agindo sobre o piloto nesse ponto só precisamos usar a segunda lei de Newton, afinal de contas já conhecemos a aceleração:
Passo 3
(c) Vamos analisar as forças que agem sobre o piloto no ponto mais baixo do círculo:
Onde é a força exercida pelo assento sobre o piloto:
Resposta
(a) na vertical para cima.
(b) , na vertical para cima.
(b) , na vertical para cima.