Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 83
Uma pedra, atirada horizontalmente do alto de uma torre de 24 m de altura, atinge o chão em um ponto que dista 18 m da base da torre. (a) Encontre a rapidez com que a pedra foi atirada. (b) Encontre a rapidez da pedra justo antes de atingir o chão.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A figura abaixo retrata o movimento do enunciado:
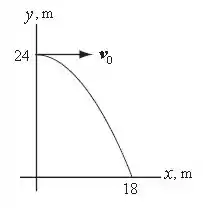
Como a pedra é atirada horizontalmente, temos que:
O tempo pode ser encontrado por:
Substituindo na equação da velocidade, temos:
Passo 2
A velocidade anted de atingir o chão é dada por:
Temos que a componente vertical é dada por:
Logo:
Substituindo os valores, temos:
Resposta
Exercícios de Livros Relacionados
Uma bola de beisebol deixa a mão do lançador horizontalmente com uma velocidade de 161k m / h . A distância até o rebatedor é 18,3m . (a) Quanto tempo a bola leva para percorrer a primeira metade da d
Na selva, um veterinário com uma arma carregada com um dardo tranquilizante e um macaco astuto de 1,5k g estão 25m acima do solo, cada qual em uma árvore a 70m de distância uma da outra. Assim que o c
O recorde atual de salto de motocicleta é de 77,0m , estabelecido por Jason Renie. Suponha que ele parta da rampa fazendo um ângulo de 12,0 ° com a horizontal e que as alturas no inicio e no final do
Um dardo é arremessado horizontalmente com uma velocidade inicial de 10m / s em direção a um ponto P , o centro de um alvo de parede. O dardo atinge um ponto Q do alvo, verticalmente abaixo de P , 0,1
Um livro de física escorrega horizontalmente para fora do topo de uma mesa com velocidade de 1,10m / s . Ele colide com o solo em 0,480s . Desprezando a resistência do ar, ache a) a altura do topo da