Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 85
O alcance de uma bala de canhão disparada horizontalmente de um morro é igual à altura do morro. Qual é a orientação do vetor velocidade do projétil ao atingir o chão? (Ignore a resistência do ar.)
Passo 1
Oi pessoal, tudo bem? Temos uma bala lançada horizontalmente. Isso significa que a velocidade inicial dela só tem componente horizontal e como não temos resistência do ar, a aceleração na horizontal é nula. Ou seja, temos velocidade constante .
Já na vertical temos a gravidade, logo temos um movimento com aceleração constante.
A figura abaixo vai nos ajudar a entender melhor o enunciado:
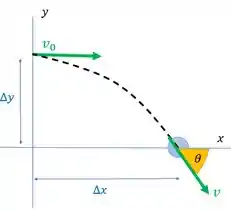
E ele pede o ângulo de chegada. Ele é o ângulo que dá a orientação do vetor velocidade no ponto onde a bala atinge o solo. A gente pode achar esse cara sabendo que as componentes dele são e :
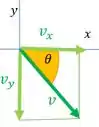
Aí usando trigonometria, podemos dizer que
O que a gente precisa fazer é achar e . Vamos lá!
Passo 2
Percebe que o enunciado fala que e tem dimensões iguais. Então vamos escrever esses dois caras.
Analisando o movimento vertical, onde temos aceleração constante, podemos pensar nessa equação:
Como inicialmente só há velocidade horizontal, temos e sabemos que (já que a gravidade aponta par abaixo). Substituindo, temos que:
Para o movimento horizontal, como temos velocidade constante, podemos usar:
Sendo que esse é :
Lembrando que o enunciado fala que e tem dimensões iguais. Mas como a bala cai, a posição final dela tem menor dimenção que a posição inicial, o que nos diz que é negativo. Mas é positivo porque a posição inicial é menor do que a final. Então a gente vai escrever:
Substituindo as expressões que achamos:
Passo 3
Falta achar .
𝐴 componente vertical da velocidade é dada pela equação horaria da velocidade quando temos aceleração constante
Lembrando que e :
Passo 4
Agora a gente substitui e na expressão de :
Logo:
Esse ângulo está no sentido horário em relação a horizontal.