Uma pedra de massa igual a 0,20 kg é libertada a partir do repouso no ponto A situado no topo de um recipiente hemisférico grande com raio R 0,50 m (Figura 7.25). Suponha que o tamanho da pedra seja pequeno em comparação com R, de modo que a pedra possa ser tratada como uma partícula, e suponha que a pedra deslize sem rolar. O trabalho realizado pela força de atrito quando ela se move de A ao ponto B situado na base do recipiente é igual a 0,22 J.
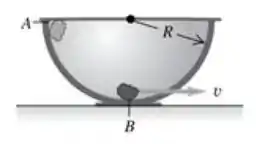
(a) Entre os pontos A e B, qual é o trabalho realizado sobre a pedra pela (i) força normal e (ii) gravidade?
(b) Qual é a velocidade da pedra quando ela atinge o ponto B?
(c) Das três forças que atuam sobre a pedra enquanto ela desliza de cima para baixo no recipiente, qual é constante (se é que existe alguma) e qual não é constante? Explique.
(d) Assim que a pedra atinge o ponto B, qual é a força normal que atua sobre ela no fundo do recipiente?
Passo 1
Opa! O enunciado nos dá a seguinte figura:
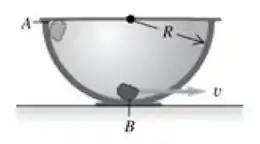
A pedra sai do ponto e vai até o ponto e o trabalho realizado pela força de atrito nesse movimento é igual a . O enunciado também nos dá os dados:
Além disso vamos desprezar as dimensões da pedra por ela ser muito menor que o raio da cuba.
Queremos o trabalho realizado sobre a pedra pela força normal e pela gravidade. Temos que o trabalho total é dado por:
Temos que , inicialmente, e ; o trabalho da força de atrito e a aceleração radial é .
Podemos desenhar o seguinte diagrama de forças:
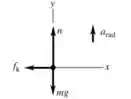
Passo 2
Vamos calcular o trabalho nos seguintes pontos, como pede a letra a!
- Pelo diagrama vemos que a força normal é perpendicular ao deslocamento, por isso não há trabalho.
- Já o trabalho da gravidade é
Passo 3
Agora vamos calcular a velocidade da pedra quando ela atinge o ponto B utilizando, de novo a fórmula do trabalho total:
Considerando todas as forças atuantes, então:
Relacionando com:
Passo 4
Para a letra “c”, a gravidade é constante e igual a . Já a normal não é constante, porque como vimos na resolução da letra a, a força normal é perpendicular ao deslocamento, por isso não há trabalho; “n” é zero em A e não zero em B.
A força de atrito não é constante, pois depende da normal.
Passo 5
Podemos calcular a força normal no ponto B, considerando
Como não temos a aceleração, faremos
Voltando,
Prontinho!
Resposta
a)
b)
c) a gravidade é constante, já a normal não é constante e a força de atrito não é constante.
d)