Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 17
(a) Uma pedra e uma pena, seguras a uma mesma altura do chão, são simultaneamente largadas. Durante os primeiros milissegundos de queda, a força de arraste sobre a pedra é menor que a força de arraste sobre a pena, mas depois, durante a queda, ocorre exatamente o oposto. Explique. (b) À luz deste resultado, explique como a aceleração da pedra é tão obviamente maior que a da pena.
Dica: Desenhe um diagrama de corpo livre para cada objeto.
Passo 1
Letra (a)
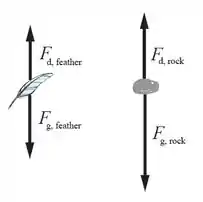
A força de arrasto depende, entre outras coisas, da velocidade do corpo e da área da sua seção transversal. Então, como a pena tem uma área frontal maior, tem uma maior força de arrasto no início. À medida que a pedra vai ganhando velocidade, sua força de arrasto vai aumentando. A pedra vai ficando mais rápida, e a força de arrasto vai aumentando junto, até ultrapassar a força de arrasto da pena.
Passo 2
Letra (b)
A velocidade terminal da pedra é bem maior do que a da pena, porque seu peso é bem maior do que o da pena (lembre-se que a força de arrasto vai aumentando até se igualar com o peso, como a gente pode ver pelo desenho). Por causa disso, a aceleração da pedra continua alta até a velocidade da pedra se aproximar da sua velocidade terminal, o que acontece antes da pena.
Resposta
Letra (a): A maior área frontal da pena predomina no início, mas depois de um tempo, a velocidade da pedra predomina.
Letra (b): A velocidade terminal da pedra é maior do que a da pena.